题解 HDOJ6514 Monitor(二维差分略记)

HDOJ

思路

一道初学者练习二维前缀和与二维差分的好题
那我顺便总结一下二维差分

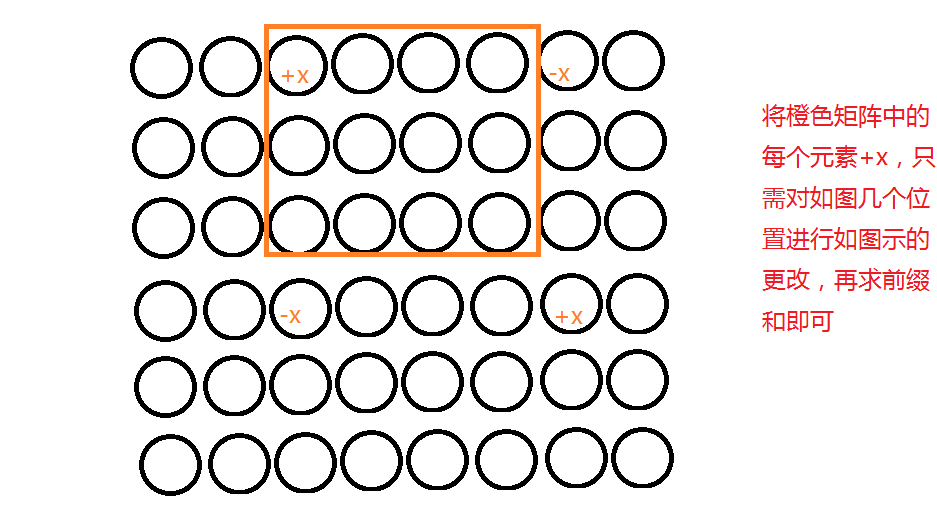
具体代码：

arr[x1,y1]+=x;
arr[x1,y2+1]-=x;
arr[x2+1,y2+1]+=x;
arr[x2+1,y1]-=x;
for(int i=1;i<=n;i++)
{
    for(int j=1;j<=m;j++)
    {
        arr[i,j]+=arr[i-1,j]+arr[i,j-1]-arr[i-1,j-1];
    }
}
//其中(x1,y1)为矩阵左上坐标，(x2,y2)为矩阵右下坐标,举个矩阵例子  
/*
  1 2 3
1 O O O
2 O O O
3 O O O
4 O O O
n=4,m=3
*/

完毕
本题只说了\(n*m<=10^{7}\)，故保险起见，开一维数组再转二维
然后就比较裸了

Code

#include<bits/stdc++.h>
using namespace std;
int arr[10000010],cntm,cntt;
int n,m,ipx1,ipy1,ipx2,ipy2;
int id(int x,int y)
{
    if(!x||!y||x>n||y>m)
        return 0;
    return (x-1)*m+y;
}
int main()
{
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        memset(arr,0,sizeof(arr));
        scanf("%d",&cntm);
        for(int i=1;i<=cntm;i++)
        {
            scanf("%d%d%d%d",&ipx1,&ipy1,&ipx2,&ipy2);
            arr[id(ipx1,ipy1)]++;
            arr[id(ipx1,ipy2+1)]--;
            arr[id(ipx2+1,ipy2+1)]++;
            arr[id(ipx2+1,ipy1)]--;
        }
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=m;j++)
            {
                arr[id(i,j)]+=arr[id(i-1,j)]+arr[id(i,j-1)]-arr[id(i-1,j-1)];
            }
        }
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=m;j++)
            {
                if(arr[id(i,j)])
                {
                    arr[id(i,j)]=1;
                }
            }
        }
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=m;j++)
            {
                arr[id(i,j)]+=arr[id(i-1,j)]+arr[id(i,j-1)]-arr[id(i-1,j-1)];
            }
        }
        scanf("%d",&cntt);
        for(int i=1;i<=cntt;i++)
        {
            scanf("%d%d%d%d",&ipx1,&ipy1,&ipx2,&ipy2);
            if(arr[id(ipx2,ipy2)]-arr[id(ipx1-1,ipy2)]-arr[id(ipx2,ipy1-1)]+arr[id(ipx1-1,ipy1-1)]==(ipx2-ipx1+1)*(ipy2-ipy1+1))
            {
                cout<<"YES"<<endl;
            }
            else
            {
                cout<<"NO"<<endl;
            }
        }
    }
}