浅谈玄学搜索A*(Astar)
蒟蒻博主自己也在学,希望写一篇新手向\(A*\),最好能帮到初学的同学们
有误请在下方评论嘲讽蒟蒻博主
更之前先放自己参考的
Upd:2019.6.15
AC的第一个A*
个人习惯用\(vector\),常数略大↓
Astar基本原理
首先,\(A*\)是再\(BFS\)的基础上加入了估价函数
说是函数也有可能是变量等,如上题,初学者大可不必退却(?)
何为估价函数?
在\(A*\)中,\(BFS\)中的队列被替换成了优先队列,而排序的依据就是当前值+当前点到终点的估值
故要保证正确,就得使估价<=实际
证明先咕着
运行起来大概是↓

举个例子,在\(k\)短路问题中,可以使i到j的估价为i到j的最短路,实现方法是反着跑最短路
题面
就像这样
#include<bits/stdc++.h>
using namespace std;
int n,m,k,st,en,dist[55],op[55];
struct edge
{
int to,dis;
};
struct node//for Dijkstra
{
int dis,pos;
bool operator < (const node &x)const
{
return x.dis<dis;
}
};
struct Anode//for Astar
{
int dis,f,pos;
vector<int>path;
bool operator < (const Anode &x)const
{
if(x.dis+x.f==dis+f)//字典序
{
int TOT=min(x.path.size(),path.size());
for(int i=0;i<TOT;i++)
{
if(path[i]!=x.path[i])
{
return path[i]>x.path[i];
}
}
}
return x.dis+x.f<dis+f;
}
};
vector<edge>a[55];//for Astar
vector<edge>b[55];//for Dijkstra
void Dijkstra(int x)
{
priority_queue<node>q;
q.push(node{0,x});
dist[x]=0;
while(!q.empty())
{
node T=q.top();
q.pop();
int now=T.pos;
if(op[now])
continue;
op[now]=1;
for(int i=0;i<b[now].size();i++)
{
if(dist[b[now][i].to]>dist[now]+b[now][i].dis)
{
dist[b[now][i].to]=dist[now]+b[now][i].dis;
if(!op[b[now][i].to])
{
q.push(node{dist[b[now][i].to],b[now][i].to});
}
}
}
}
}
int Astar(int x)
{
priority_queue<Anode>q;
Anode start;
start.dis=0;
start.f=dist[x];
start.pos=x;
start.path.push_back(x);
q.push(start);
int nowk=0;
while(!q.empty())
{
Anode T=q.top();
q.pop();
int now=T.pos;
if(now==en)
{
nowk++;
}
if(nowk>=k)
{
int tot=T.path.size();
for(int i=0;i<tot;i++)
{
cout<<T.path[i];
if(i!=tot-1)
{
cout<<"-";
}
}
return T.dis;
}
int Size=a[now].size();
for(int i=0;i<Size;i++)
{
edge t=a[now][i];
int flag=0;
for(int j=0;j<T.path.size();j++)
{
if(T.path[j]==t.to)
{
flag=1;
break;
}
}
if(flag)
{
continue;
}
Anode tmp;
tmp=T;
tmp.dis=T.dis+t.dis;
tmp.f=dist[t.to];
tmp.pos=t.to;
tmp.path.push_back(t.to);
q.push(tmp);
}
}
cout<<"No";
return 0;
}
int main()
{
cin>>n>>m>>k>>st>>en;
int ip1,ip2,ip3;
if(n==30&&m==759)//有个点卡Astar
{
cout<<"1-3-10-26-2-30";
return 0;
}
for(int i=1;i<=m;i++)
{
cin>>ip1>>ip2>>ip3;
a[ip1].push_back(edge{ip2,ip3});
b[ip2].push_back(edge{ip1,ip3});//反向最短路
}
for(int i=0;i<=51;i++)
{
dist[i]=2147483647;
}
Dijkstra(en);//源点也要反
Astar(st);
}
看不懂?正常
看懂了?恭喜,您可以忽略这篇博文了
现在讲解一下估价
我们讲过

至于为什么证明要咕着?很简单,当时我还没想好
证明
可以这样理解:
先脑补一个最短路问题,设估价皆<=实际
若先搜到一个点,其目前经过+估值最小,而实际上并非如此
我们可以看到,在\(A*\)的搜索中,越往后搜越接近实际情况
显而易见吧
所以,预估小的点先进队(不由想到省选)后,会拓展其邻近节点,然后一会儿之后,队列中大部分都是这个点的拓展点了
但是,很久之后,当那个并非最短路经过的点渐渐真实(该点实际与预估相差较大),其预估+目前就会被其他点超过,而变得不再优先,落寞地在队尾等
所以一个点如果非最优解,ta就不会一直拓展下去,所以先到终点的必为最优解
回到刚才那个问题,为什么预估<=实际?
我们回顾刚才的讲解


如果估价>实际,则一些原本要超越错解的点无法超过,导致搜到错误答案
试想一下,如果正解中的一个点估价为\(INF\),ta是不是得最后更新?
到ta更新的时候早\(WA\)了
胡扯完毕证毕
复杂度分析
\(A*\)是\(BFS\)的优化,优化成什么样,得看估价函数的设计(所以\(A*\)的灵魂就是估价函数)
估价函数越接近实际,时间越少
举个极端的例子:
估价=实际
在这种情况中,无用节点基本(注意!)不会进队
画张图?
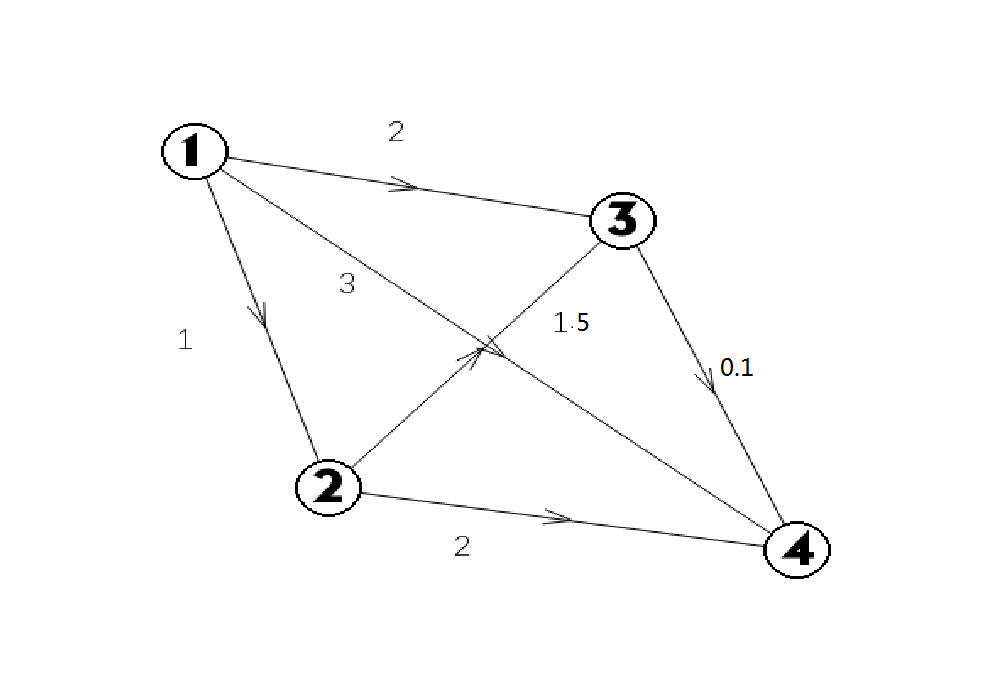
(起点\(1\),终点\(4\))
在这种情况中,从\(1\)第一次枚举,所有相连点进队,而下次会先拓展\(3\)的相连点
广而言之,当估价=实际时,\(A*\)只会拓展正确路径,将与正确路径直接相连的节点入队
常用估价函数
坐标图:欧几里得距离
网格图:曼哈顿距离
\(k\)短路:反向图跑最短路
Tips
若预估一直等于\(0\),则算法退化成\(Dijkstra\)
若\(TLE\),则需更换估价函数
若还是\(TLE\),吸吸氧卡卡常就过了
另一个应用:八数码
题面
此题就是将整个矩阵视为状态,然后以各点位置与目标状态位置的曼哈顿距离之和作为估价函数
题解
#include<bits/stdc++.h>
using namespace std;
int arr[10],vis[10],A[10],fac[10],a[10],L[10],R[10],ans,n;
bool flag[10000010];
char ip;
struct node
{
int h[10],d,f;
vector<int>pre;
bool operator < (const node &x)const
{
return x.d+x.f<d+f;
}
};
int C_hash()//Cantor Expansion
{
int res=0,sum=0;
for(int i=1;i<9;i++)
{
for(int j=i+1;j<=9;j++)
{
if(arr[j]<arr[i])
{
sum++;
}
}
res+=sum*fac[9-i];
sum=0;
}
return res+1;
}
int calc()
{
int ans=0;
for(int i=1;i<=9;i++)
{
if(arr[i]==9)
{
continue;
}
ans+=abs(((i-1)%3+1)-((arr[i]-1)%3+1))+abs(((i-1)/3+1)-((arr[i]-1)/3+1));
}
return ans;
}
priority_queue<node>q;
void Astar()
{
while(!q.empty())
{
node T=q.top();
int D=q.top().d;
int F=q.top().f;
q.pop();
for(int i=1;i<=9;i++)
{
arr[i]=T.h[i];
}
int HASH=C_hash();
if(flag[HASH])
{
continue;
}
else
{
flag[HASH]=1;
}
if(!calc())
{
for(int i=0;i<T.pre.size();i++)
{
if(T.pre[i]==1)
{
cout<<"u";
}
if(T.pre[i]==2)
{
cout<<"d";
}
if(T.pre[i]==3)
{
cout<<"l";
}
if(T.pre[i]==4)
{
cout<<"r";
}
}
return ;
}
int X;
for(int i=1;i<=9;i++)
{
if(arr[i]==9)
{
X=i;
break;
}
}
if(X>3)
{
swap(T.h[X],T.h[X-3]);
T.f=calc();
T.d=D+1;
T.pre.push_back(1);
q.push(T);
T.pre.pop_back();
swap(T.h[X],T.h[X-3]);
}
if(X<7)
{
swap(T.h[X],T.h[X+3]);
T.f=calc();
T.d=D+1;
T.pre.push_back(2);
q.push(T);
T.pre.pop_back();
swap(T.h[X],T.h[X+3]);
}
if((X-1)%3+1>1)
{
swap(T.h[X],T.h[X-1]);
T.f=calc();
T.d=D+1;
T.pre.push_back(3);
q.push(T);
T.pre.pop_back();
swap(T.h[X],T.h[X-1]);
}
if((X-1)%3+1<3)
{
swap(T.h[X],T.h[X+1]);
T.f=calc();
T.d=D+1;
T.pre.push_back(4);
q.push(T);
T.pre.pop_back();
swap(T.h[X],T.h[X+1]);
}
}
}
int mergesort(int l,int mid,int r)
{
int n1,n2;
n1=mid-l+1;
n2=r-mid;
for(int i=1;i<=n1;i++)
{
L[i]=a[i+l-1];
}
for(int i=1;i<=n2;i++)
{
R[i]=a[mid+i];
}
L[n1+1]=-999999999;
R[n2+1]=-999999999;
int q1=1,q2=1;
for(;q2<=n2;)
{
if(L[q1]>R[q2])
{
ans+=n2-q2+1;
q1++;
}
else
{
q2++;
}
}
q1=1,q2=1;
for(int i=l;i<=r;i++)
{
if(L[q1]>=R[q2])
{
a[i]=L[q1];
q1++;
}
else
{
a[i]=R[q2];
q2++;
}
}
}
int merge(int l,int r)
{
if(l<r)
{
int mid=(l+r)/2;
merge(l,mid);
merge(mid+1,r);
mergesort(l,mid,r);
}
return 0;
}
int main()
{
fac[0]=1;
for(int i=1;i<=9;i++)
{
fac[i]=fac[i-1]*i;
}
for(int i=1;i<=3;i++)
{
for(int j=1;j<=3;j++)
{
cin>>ip;
if('1'<=ip&&ip<='8')
{
arr[(i-1)*3+j]=ip-'0';
}
else
{
arr[(i-1)*3+j]=9;
}
}
}
for(int i=1;i<=9;i++)
{
if(arr[i]!=9)
{
a[++n]=arr[i];
}
}
merge(1,n);
int mod1=ans%2;
ans=0;
n=0;
for(int i=1;i<=8;i++)
{
a[i]=i;
}
merge(1,n);
int mod2=ans%2;
if(mod1!=mod2)
{
cout<<"unsolvable";
return 0;
}
node T;
for(int i=1;i<=9;i++)
{
T.h[i]=arr[i];
}
T.d=0;
T.f=calc();
q.push(T);
Astar();
}
IDAstar
半骗分
题面
Code
#include<bits/stdc++.h>
using namespace std;
int T,n,a[16],ans;
int IDAstar(int now)
{
if(now>ans)
{
return 0;
}
for(int l=1;l<=n-1;l++)
{
for(int i=1;i<=n-l;i++)
{
for(int j=i+l;j<=n;j++)
{
int tmp[16];
for(int k=1;k<=n;k++)
{
tmp[k]=a[k];
}
for(int k=i+l;k<=j;k++)
{
a[k-l]=tmp[k];
}
for(int k=0;k<l;k++)
{
a[j-l+k+1]=tmp[i+k];
}
int tot=0;
for(int k=1;k<=n;k++)
{
if(a[k]!=k)
{
tot++;
}
}
if(!tot)
{
return 1;
}
if(3*(ans-now)<tot-2)
{
for(int k=1;k<=n;k++)
{
a[k]=tmp[k];
}
continue;
}
if(IDAstar(now+1))
return 1;
for(int k=1;k<=n;k++)
{
a[k]=tmp[k];
}
}
}
}
return 0;
}
int main()
{
cin>>T;
while(T--)
{
cin>>n;
int tot=0;
for(int i=1;i<=n;i++)
{
cin>>a[i];
if(a[i]!=i)
{
tot++;
}
}
if(!tot)
{
cout<<0<<endl;
continue;
}
ans=1;
while(ans<5&&!IDAstar(1))
{
ans++;
}
if(ans==5)
{
cout<<"5 or more"<<endl;
continue;
}
cout<<ans<<endl;
}
}
/*
3
9
6 1 9 8 3 5 2 4 7
9
9 8 7 4 5 6 2 1 3
9
3 2 7 6 4 8 9 5 1
*/


