二叉树的遍历（递归实现）【摘录自严长生老师的网站】

根据访问结点时机的不同，分为三种遍历方式：

• 先访问根结点，再遍历左右子树，称为“先序遍历”；
• 遍历左子树，之后访问根结点，然后遍历右子树，称为“中序遍历”；
• 遍历完左右子树，再访问根结点，称为“后序遍历”。

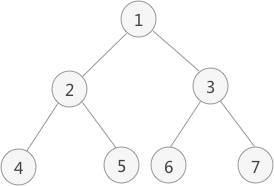
以上图为例

先序遍历：1 2 4 5 3 6 7

中序遍历：4 2 5 1 6 3 7

后序遍历：4 5 2 6 7 3 1

代码实现

#include <stdio.h>
#include <string.h>
#define TElemType int
//构造结点的结构体
typedef struct BiTNode{
    TElemType data;//数据域
    struct BiTNode *lchild,*rchild;//左右孩子指针
}BiTNode,*BiTree;
//初始化树的函数
void CreateBiTree(BiTree *T){
    *T=(BiTNode*)malloc(sizeof(BiTNode));
    (*T)->data=1;
    (*T)->lchild=(BiTNode*)malloc(sizeof(BiTNode));
    (*T)->rchild=(BiTNode*)malloc(sizeof(BiTNode));
  
    (*T)->lchild->data=2;
    (*T)->lchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));
    (*T)->lchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));
    (*T)->lchild->rchild->data=5;
    (*T)->lchild->rchild->lchild=NULL;
    (*T)->lchild->rchild->rchild=NULL;
    (*T)->rchild->data=3;
    (*T)->rchild->lchild=(BiTNode*)malloc(sizeof(BiTNode));
    (*T)->rchild->lchild->data=6;
    (*T)->rchild->lchild->lchild=NULL;
    (*T)->rchild->lchild->rchild=NULL;
    (*T)->rchild->rchild=(BiTNode*)malloc(sizeof(BiTNode));
    (*T)->rchild->rchild->data=7;
    (*T)->rchild->rchild->lchild=NULL;
    (*T)->rchild->rchild->rchild=NULL;
    (*T)->lchild->lchild->data=4;
    (*T)->lchild->lchild->lchild=NULL;
    (*T)->lchild->lchild->rchild=NULL;
}
//模拟操作结点元素的函数，输出结点本身的数值
void displayElem(BiTNode* elem){
    printf("%d ",elem->data);
}
//先序遍历
void PreOrderTraverse(BiTree T){
    if (T) {
        displayElem(T);//调用操作结点数据的函数方法
        PreOrderTraverse(T->lchild);//访问该结点的左孩子
        PreOrderTraverse(T->rchild);//访问该结点的右孩子
    }
    //如果结点为空，返回上一层
    return;
}
//中序遍历
void INOrderTraverse(BiTree T){
    if (T) {
        INOrderTraverse(T->lchild);//遍历左孩子
        displayElem(T);//调用操作结点数据的函数方法
        INOrderTraverse(T->rchild);//遍历右孩子
    }
    //如果结点为空，返回上一层
    return;
}
//后序遍历
void PostOrderTraverse(BiTree T){
    if (T) {
        PostOrderTraverse(T->lchild);//遍历左孩子
        PostOrderTraverse(T->rchild);//遍历右孩子
        displayElem(T);//调用操作结点数据的函数方法
    }
    //如果结点为空，返回上一层
    return;
}
int main() {
    BiTree Tree;
    CreateBiTree(&Tree);
    printf("前序遍历: \n");
    PreOrderTraverse(Tree);
    printf("\n中序遍历算法: \n");
    INOrderTraverse(Tree);
    printf("\n后序遍历: \n");
    PostOrderTraverse(Tree);
}

输出

前序遍历:
1 2 4 5 3 6 7
中序遍历算法:
4 2 5 1 6 3 7
后序遍历:
4 5 2 6 7 3 1