最小生成树[摘录自严长生老师的网站]
最小生成树的对象是无向连通网,这个前提是必要的,无向,邻接矩阵是对称的,连通,点与点之间两两可达,网,所有边都有权重,对应于城市修路问题,就是路的长度,最小生成树,对应同时满足城市之间连通和修路花费最小,是一个实际应用性很强的算法。
最小生成树的实现主要有两种算法,Prim算法和Kruskal算法,下面分别介绍这两种算法,及其C语言实现。
1. Prim
首先定义无向网,采用邻接矩阵的存储方式,个人认为采用邻接表也可以,而且可以节省不少空间
#include <stdio.h>
#include <stdlib.h>
#define VertexType int
#define VRType int
#define MAX_VERtEX_NUM 20
#define InfoType char
#define INFINITY 65535
typedef struct {
VRType adj; //对于无权图,用 1 或 0 表示是否相邻;对于带权图,直接为权值。
InfoType * info; //弧额外含有的信息指针
}ArcCell,AdjMatrix[MAX_VERtEX_NUM][MAX_VERtEX_NUM];
typedef struct {
VertexType vexs[MAX_VERtEX_NUM]; //存储图中顶点数据
AdjMatrix arcs; //二维数组,记录顶点之间的关系
int vexnum,arcnum; //记录图的顶点数和弧(边)数
}MGraph;
//根据顶点本身数据,判断出顶点在二维数组中的位置
int LocateVex(MGraph G,VertexType v){
int i=0;
//遍历一维数组,找到变量v
for (; i<G.vexnum; i++) {
if (G.vexs[i]==v) {
return i;
}
}
return -1;
}
然后创建无向网,相互之间不连接的顶点,邻接矩阵权值设为最大整数,这里代表着无穷大。
//构造无向网
void CreateUDN(MGraph* G){
scanf("%d,%d",&(G->vexnum),&(G->arcnum));
for (int i=0; i<G->vexnum; i++) {
scanf("%d",&(G->vexs[i]));
}
for (int i=0; i<G->vexnum; i++) {
for (int j=0; j<G->vexnum; j++) {
G->arcs[i][j].adj=INFINITY;
G->arcs[i][j].info=NULL;
}
}
for (int i=0; i<G->arcnum; i++) {
int v1,v2,w;
scanf("%d,%d,%d",&v1,&v2,&w);
int m=LocateVex(*G, v1);
int n=LocateVex(*G, v2);
if (m==-1 ||n==-1) {
printf("no this vertex\n");
return;
}
G->arcs[n][m].adj=w;
G->arcs[m][n].adj=w;
}
}
然后要建立辅助数组,这里的辅助数组是针对每个顶点,如果已经在最小生成树中,权值设为0,否则设为距当前最小生成树的最小距离
//辅助数组,用于每次筛选出权值最小的边的邻接点
typedef struct {
VertexType adjvex;//记录权值最小的边的起始点
VRType lowcost;//记录该边的权值
}closedge[MAX_VERtEX_NUM];
closedge theclose;//创建一个全局数组,因为每个函数中都会使用到
//在辅助数组中找出权值最小的边的数组下标,就可以间接找到此边的终点顶点。
int minimun(MGraph G,closedge close){
int min=INFINITY;
int min_i=-1;
for (int i=0; i<G.vexnum; i++) {
//权值为0,说明顶点已经归入最小生成树中;然后每次和min变量进行比较,最后找出最小的。
if (close[i].lowcost>0 && close[i].lowcost < min) {
min=close[i].lowcost;
min_i=i;
}
}
//返回最小权值所在的数组下标
return min_i;
}
最后是主体函数,根据给定的初始顶点,初始化辅助数组,然后不断迭代n-1次
//普里姆算法函数,G为无向网,u为在网中选择的任意顶点作为起始点
void miniSpanTreePrim(MGraph G,VertexType u){
//找到该起始点在顶点数组中的位置下标
int k=LocateVex(G, u);
//首先将与该起始点相关的所有边的信息:边的起始点和权值,存入辅助数组中相应的位置,例如(1,2)边,adjvex为0,lowcost为6,存入theclose[1]中,辅助数组的下标表示该边的顶点2
for (int i=0; i<G.vexnum; i++) {
if (i !=k) {
theclose[i].adjvex=k;
theclose[i].lowcost=G.arcs[k][i].adj;
}
}
//由于起始点已经归为最小生成树,所以辅助数组对应位置的权值为0,这样,遍历时就不会被选中
theclose[k].lowcost=0;
//选择下一个点,并更新辅助数组中的信息
for (int i=1; i<G.vexnum; i++) {
//找出权值最小的边所在数组下标
k=minimun(G, theclose);
//输出选择的路径
printf("v%d v%d\n",G.vexs[theclose[k].adjvex],G.vexs[k]);
//归入最小生成树的顶点的辅助数组中的权值设为0
theclose[k].lowcost=0;
//更新辅助数组中存储的信息,由于此时树中新加入了一个顶点,需要判断,由此顶点出发,到达其它各顶点的权值是否比之前记录的权值还要小,如果还小,则更新
for (int j=0; j<G.vexnum; j++) {
if (G.arcs[k][j].adj<theclose[j].lowcost) {
theclose[j].adjvex=k;
theclose[j].lowcost=G.arcs[k][j].adj;
}
}
}
printf("\n");
}
int main(){
MGraph G;
CreateUDN(&G);
miniSpanTreePrim(G, 1);
}
2.Kruskal
相比于Prim算法,Kruskal算法更适合边比较少的无向网,因为Kruskal是关于边的算法,算法的初始状态是一张没有边但顶点与无向网相同的图,然后逐步向图中添加边,添加满n-1条边,算法告成,我觉得比Prim算法更简单直观些。
所以克鲁斯卡尔算法的具体思路是:将所有边按照权值的大小进行升序排序,然后从小到大一一判断,条件为:如果这个边不会与之前选择的所有边组成回路,就可以作为最小生成树的一部分;反之,舍去。直到具有 n 个顶点的连通网筛选出来 n-1 条边为止。筛选出来的边和所有的顶点构成此连通网的最小生成树。
如何判断是否存在回路呢,其实比较简单,初始时对所有顶点做标记,每个顶点标记都不同,然后选择一条最短的边,并将边的两端顶点置为相同的标记,标记相同,代表着连通,所以如果你选择的边,两端顶点已经连通的话,那末放弃这条边,继续迭代。
以下面的图为例。
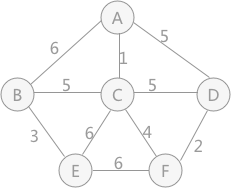
对顶点进行标记,这里用颜色标记
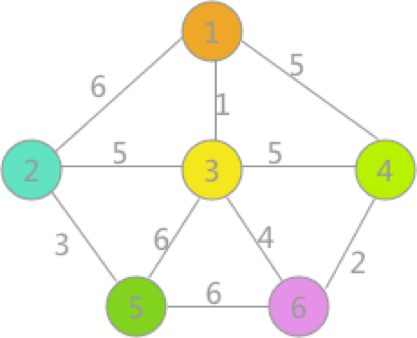
接着对边排序,然后从最短的边开始迭代
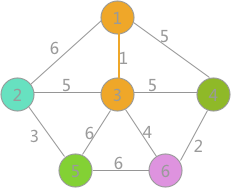

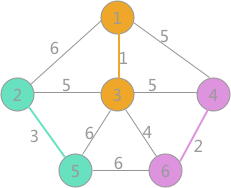
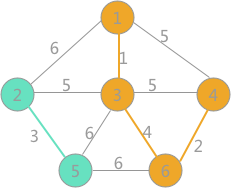
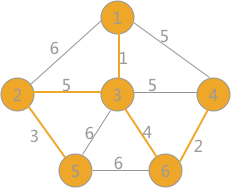
当边的数目为n-1时,算法结束。
下面是代码实现。
#include "stdio.h"
#include "stdlib.h"
#define MAX_VERtEX_NUM 20
#define VertexType int
typedef struct edge{
VertexType initial;
VertexType end;
VertexType weight;
}edge[MAX_VERtEX_NUM];
//定义辅助数组
typedef struct {
VertexType value;//顶点数据
int sign;//每个顶点所属的集合
}assist[MAX_VERtEX_NUM];
assist assists;
//qsort排序函数中使用,使edges结构体中的边按照权值大小升序排序
int cmp(const void *a,const void*b){
return ((struct edge*)a)->weight-((struct edge*)b)->weight;
}
//初始化连通网
void CreateUDN(edge *edges,int *vexnum,int *arcnum){
printf("输入连通网的边数:\n");
scanf("%d %d",&(*vexnum),&(*arcnum));
printf("输入连通网的顶点:\n");
for (int i=0; i<(*vexnum); i++) {
scanf("%d",&(assists[i].value));
assists[i].sign=i;
}
printf("输入各边的起始点和终点及权重:\n");
for (int i=0 ; i<(*arcnum); i++) {
scanf("%d,%d,%d",&(*edges)[i].initial,&(*edges)[i].end,&(*edges)[i].weight);
}
}
//在assists数组中找到顶点point对应的位置下标
int Locatevex(int vexnum,int point){
for (int i=0; i<vexnum; i++) {
if (assists[i].value==point) {
return i;
}
}
return -1;
}
int main(){
int arcnum,vexnum;
edge edges;
CreateUDN(&edges,&vexnum,&arcnum);
//对连通网中的所有边进行升序排序,结果仍保存在edges数组中
qsort(edges, arcnum, sizeof(edges[0]), cmp);
//创建一个空的结构体数组,用于存放最小生成树
edge minTree;
//设置一个用于记录最小生成树中边的数量的常量
int num=0;
//遍历所有的边
for (int i=0; i<arcnum; i++) {
//找到边的起始顶点和结束顶点在数组assists中的位置
int initial=Locatevex(vexnum, edges[i].initial);
int end=Locatevex(vexnum, edges[i].end);
//如果顶点位置存在且顶点的标记不同,说明不在一个集合中,不会产生回路
if (initial!=-1&& end!=-1&&assists[initial].sign!=assists[end].sign) {
//记录该边,作为最小生成树的组成部分
minTree[num]=edges[i];
//计数+1
num++;
//将新加入生成树的顶点标记全不更改为一样的
for (int k=0; k<vexnum; k++) {
if (assists[k].sign==assists[end].sign) {
assists[k].sign=assists[initial].sign;
}
}
//如果选择的边的数量和顶点数相差1,证明最小生成树已经形成,退出循环
if (num==vexnum-1) {
break;
}
}
}
//输出语句
for (int i=0; i<vexnum-1; i++) {
printf("%d,%d\n",minTree[i].initial,minTree[i].end);
}
return 0;
}
输出
输入连通网的边数: 6 10 输入连通网的顶点: 1 2 3 4 5 6 输入各边的起始点和终点及权重: 1,2,6 1,3,1 1,4,5 2,3,5 2,5,3 3,4,5 3,5,6 3,6,4 4,6,2 5,6,6 1,3 4,6 2,5 3,6 2,3



 浙公网安备 33010602011771号
浙公网安备 33010602011771号