图的顺序存储(邻接矩阵存储)【摘录自严长生老师的网站】
图是表达多对多关系的一种数据结构,组成要素为顶点和连接顶点的边。
根据边有无方向可分为有向图和无向图
当边有权重时,升级为有向网和无向网
图在存储时,可采用邻接矩阵,比如下面的无向图(A)和(B)
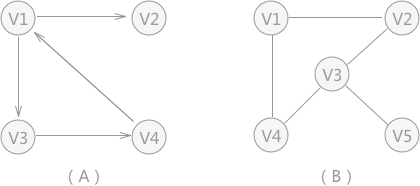
用邻接矩阵可分别表示为下面这样


每一行代表一个顶点,每一列也对应一个顶点,对于无向图,边没有方向,顶点之间相互连接,则对应位置设为1,否则为0,无向图的邻接矩阵是对称的。
对于有向图,边是有方向的,所以有向图的边不叫边,叫有向边或者弧,个人觉得有向边更直观,那么有向图的行,代表着该顶点到达哪些顶点,可达的记为1,否则为0,有向图的列,代表着该顶点可由哪些顶点到达,可达的记为1,否则为0。
有了这些基本概念,就可以基于C语言实现其存储了,注意,这里采用的是邻接矩阵的存储方式。
上代码。
#include <stdio.h>
#define MAX_VERtEX_NUM 20 //顶点的最大个数
#define VRType int //表示顶点之间的关系的变量类型
#define InfoType char //存储弧或者边额外信息的指针变量类型
#define VertexType int //图中顶点的数据类型
typedef enum{DG,DN,UDG,UDN}GraphKind; //枚举图的 4 种类型
typedef struct {
VRType adj; //对于无权图,用 1 或 0 表示是否相邻;对于带权图,直接为权值。
InfoType * info; //弧或边额外含有的信息指针
}ArcCell,AdjMatrix[MAX_VERtEX_NUM][MAX_VERtEX_NUM];
typedef struct {
VertexType vexs[MAX_VERtEX_NUM]; //存储图中顶点数据
AdjMatrix arcs; //二维数组,记录顶点之间的关系
int vexnum,arcnum; //记录图的顶点数和弧(边)数
GraphKind kind; //记录图的种类
}MGraph;
//根据顶点本身数据,判断出顶点在二维数组中的位置
int LocateVex(MGraph * G,VertexType v){
int i=0;
//遍历一维数组,找到变量v
for (; i<G->vexnum; i++) {
if (G->vexs[i]==v) {
break;
}
}
//如果找不到,输出提示语句,返回-1
if (i>G->vexnum) {
printf("no such vertex.\n");
return -1;
}
return i;
}
//构造有向图
void CreateDG(MGraph *G){
//输入图含有的顶点数和弧的个数
scanf("%d,%d",&(G->vexnum),&(G->arcnum));
//依次输入顶点本身的数据
for (int i=0; i<G->vexnum; i++) {
scanf("%d",&(G->vexs[i]));
}
//初始化二维矩阵,全部归0,指针指向NULL
for (int i=0; i<G->vexnum; i++) {
for (int j=0; j<G->vexnum; j++) {
G->arcs[i][j].adj=0;
G->arcs[i][j].info=NULL;
}
}
//在二维数组中添加弧的数据
for (int i=0; i<G->arcnum; i++) {
int v1,v2;
//输入弧头和弧尾
scanf("%d,%d",&v1,&v2);
//确定顶点位置
int n=LocateVex(G, v1);
int m=LocateVex(G, v2);
//排除错误数据
if (m==-1 ||n==-1) {
printf("no this vertex\n");
return;
}
//将正确的弧的数据加入二维数组
G->arcs[n][m].adj=1;
}
}
//构造无向图
void CreateDN(MGraph *G){
scanf("%d,%d",&(G->vexnum),&(G->arcnum));
for (int i=0; i<G->vexnum; i++) {
scanf("%d",&(G->vexs[i]));
}
for (int i=0; i<G->vexnum; i++) {
for (int j=0; j<G->vexnum; j++) {
G->arcs[i][j].adj=0;
G->arcs[i][j].info=NULL;
}
}
for (int i=0; i<G->arcnum; i++) {
int v1,v2;
scanf("%d,%d",&v1,&v2);
int n=LocateVex(G, v1);
int m=LocateVex(G, v2);
if (m==-1 ||n==-1) {
printf("no this vertex\n");
return;
}
G->arcs[n][m].adj=1;
G->arcs[m][n].adj=1;//无向图的二阶矩阵沿主对角线对称
}
}
//构造有向网,和有向图不同的是二阶矩阵中存储的是权值。
void CreateUDG(MGraph *G){
scanf("%d,%d",&(G->vexnum),&(G->arcnum));
for (int i=0; i<G->vexnum; i++) {
scanf("%d",&(G->vexs[i]));
}
for (int i=0; i<G->vexnum; i++) {
for (int j=0; j<G->vexnum; j++) {
G->arcs[i][j].adj=0;
G->arcs[i][j].info=NULL;
}
}
for (int i=0; i<G->arcnum; i++) {
int v1,v2,w;
scanf("%d,%d,%d",&v1,&v2,&w);
int n=LocateVex(G, v1);
int m=LocateVex(G, v2);
if (m==-1 ||n==-1) {
printf("no this vertex\n");
return;
}
G->arcs[n][m].adj=w;
}
}
//构造无向网。和无向图唯一的区别就是二阶矩阵中存储的是权值
void CreateUDN(MGraph* G){
scanf("%d,%d",&(G->vexnum),&(G->arcnum));
for (int i=0; i<G->vexnum; i++) {
scanf("%d",&(G->vexs[i]));
}
for (int i=0; i<G->vexnum; i++) {
for (int j=0; j<G->vexnum; j++) {
G->arcs[i][j].adj=0;
G->arcs[i][j].info=NULL;
}
}
for (int i=0; i<G->arcnum; i++) {
int v1,v2,w;
scanf("%d,%d,%d",&v1,&v2,&w);
int m=LocateVex(G, v1);
int n=LocateVex(G, v2);
if (m==-1 ||n==-1) {
printf("no this vertex\n");
return;
}
G->arcs[n][m].adj=w;
G->arcs[m][n].adj=w;//矩阵对称
}
}
void CreateGraph(MGraph *G){
//选择图的类型
scanf("%d",&(G->kind));
//根据所选类型,调用不同的函数实现构造图的功能
switch (G->kind) {
case DG:
return CreateDG(G);
break;
case DN:
return CreateDN(G);
break;
case UDG:
return CreateUDG(G);
break;
case UDN:
return CreateUDN(G);
break;
default:
break;
}
}
//输出函数
void PrintGrapth(MGraph G)
{
for (int i = 0; i < G.vexnum; i++)
{
for (int j = 0; j < G.vexnum; j++)
{
printf("%d ", G.arcs[i][j].adj);
}
printf("\n");
}
}
int main() {
MGraph G;//建立一个图的变量
CreateGraph(&G);//调用创建函数,传入地址参数
PrintGrapth(G);//输出图的二阶矩阵
return 0;
}
以下面这张图为例
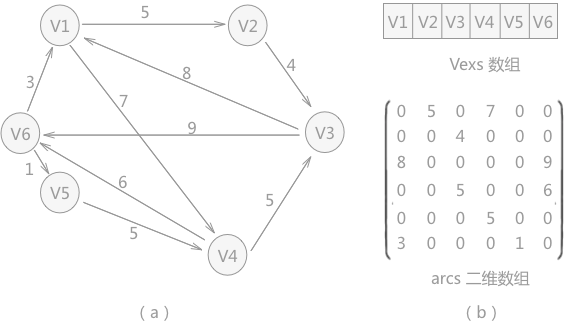
对应的输入输出为
2 6,10 1 2 3 4 5 6 1,2,5 2,3,4 3,1,8 1,4,7 4,3,5 3,6,9 6,1,3 4,6,6 6,5,1 5,4,5 0 5 0 7 0 0 0 0 4 0 0 0 8 0 0 0 0 9 0 0 5 0 0 6 0 0 0 5 0 0 3 0 0 0 1 0
这是按照邻接矩阵来存储的,邻接矩阵的空间开销是固定的,因此当矩阵比较稠密时比较划算,当顶点之间的连接比较稀疏时,采用邻接表更合适。



