【推荐系统】neural_collaborative_filtering(源码解析)
很久没看推荐系统相关的论文了,最近发现一篇2017年的论文,感觉不错。
原始论文 https://arxiv.org/pdf/1708.05031.pdf
网上有翻译了 https://www.cnblogs.com/HolyShine/p/6728999.html
git项目 https://github.com/hexiangnan/neural_collaborative_filtering
项目的主题框架如下:
代码是使用keras来实现的深度学习,其中GMF.py是传统的Matrix Factorization算法,关键代码分为两部分:
def get_model(num_users, num_items, latent_dim, regs=[0,0]): # Input variables user_input = Input(shape=(1,), dtype='int32', name = 'user_input') item_input = Input(shape=(1,), dtype='int32', name = 'item_input') MF_Embedding_User = Embedding(input_dim = num_users, output_dim = latent_dim, name = 'user_embedding', init = init_normal, W_regularizer = l2(regs[0]), input_length=1) MF_Embedding_Item = Embedding(input_dim = num_items, output_dim = latent_dim, name = 'item_embedding', init = init_normal, W_regularizer = l2(regs[1]), input_length=1) # Crucial to flatten an embedding vector! user_latent = Flatten()(MF_Embedding_User(user_input)) item_latent = Flatten()(MF_Embedding_Item(item_input)) # Element-wise product of user and item embeddings predict_vector = merge([user_latent, item_latent], mode = 'mul') # Final prediction layer #prediction = Lambda(lambda x: K.sigmoid(K.sum(x)), output_shape=(1,))(predict_vector) prediction = Dense(1, activation='sigmoid', init='lecun_uniform', name = 'prediction')(predict_vector) model = Model(input=[user_input, item_input], output=prediction) return model
上述代码是构建模型结构,首先定义Input为一维多列的数据,然后是Embedding层,Embedding主要是为了降维,就是起到了look up的作用,然后是Merge层,将用户和物品的张量进行了内积相乘(latent_dim 表示两者的潜在降维的维度是相同的,因此可以做内积),紧接着是一个全连接层,激活函数为sigmoid。
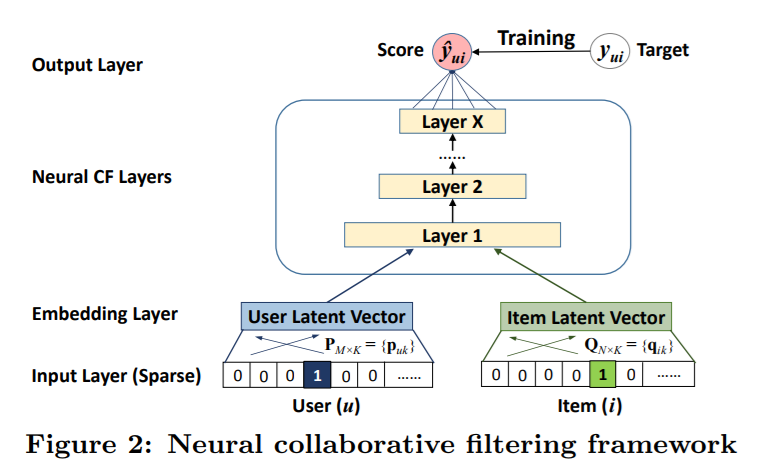
下面是MLP.py的源码:
def get_model(num_users, num_items, layers = [20,10], reg_layers=[0,0]): assert len(layers) == len(reg_layers) num_layer = len(layers) #Number of layers in the MLP # Input variables user_input = Input(shape=(1,), dtype='int32', name = 'user_input') item_input = Input(shape=(1,), dtype='int32', name = 'item_input') MLP_Embedding_User = Embedding(input_dim = num_users, output_dim = layers[0]/2, name = 'user_embedding', init = init_normal, W_regularizer = l2(reg_layers[0]), input_length=1) MLP_Embedding_Item = Embedding(input_dim = num_items, output_dim = layers[0]/2, name = 'item_embedding', init = init_normal, W_regularizer = l2(reg_layers[0]), input_length=1) # Crucial to flatten an embedding vector! user_latent = Flatten()(MLP_Embedding_User(user_input)) item_latent = Flatten()(MLP_Embedding_Item(item_input)) # The 0-th layer is the concatenation of embedding layers vector = merge([user_latent, item_latent], mode = 'concat') # MLP layers for idx in xrange(1, num_layer): layer = Dense(layers[idx], W_regularizer= l2(reg_layers[idx]), activation='relu', name = 'layer%d' %idx) vector = layer(vector) # Final prediction layer prediction = Dense(1, activation='sigmoid', init='lecun_uniform', name = 'prediction')(vector) model = Model(input=[user_input, item_input], output=prediction) return model
最重要的也是构建模型的部分,与GMF不同的有两个部分,首先是user_latent和item_latent的merge的部分,不再采用内积的形式,而是contract拼接的方式;再者就是for循环构建深层全连接神经网络,内部Layer的激活函数是relu,最后一层的激活函数仍然是sigmoid。
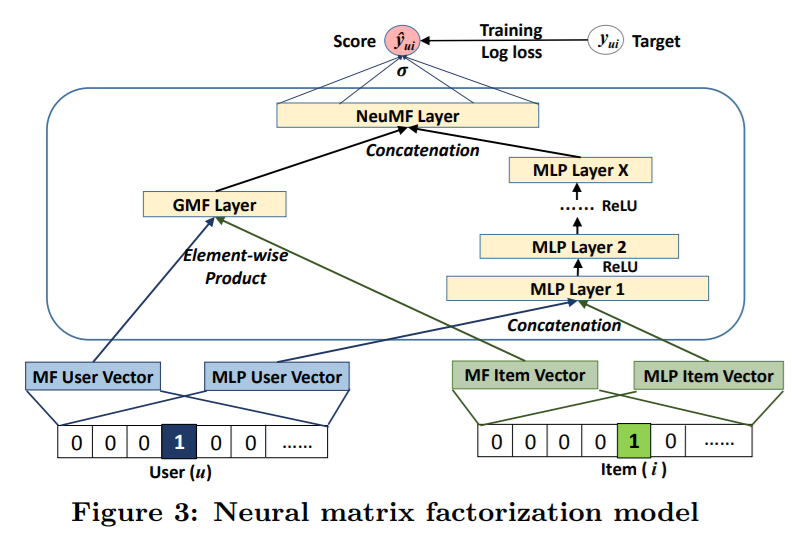
接下来是NeuMF.py,将MLP和GMF进行了融合,模型构建代码如下
def get_model(num_users, num_items, mf_dim=10, layers=[10], reg_layers=[0], reg_mf=0): assert len(layers) == len(reg_layers) num_layer = len(layers) #Number of layers in the MLP # Input variables user_input = Input(shape=(1,), dtype='int32', name = 'user_input') item_input = Input(shape=(1,), dtype='int32', name = 'item_input') # Embedding layer MF_Embedding_User = Embedding(input_dim = num_users, output_dim = mf_dim, name = 'mf_embedding_user', init = init_normal, W_regularizer = l2(reg_mf), input_length=1) MF_Embedding_Item = Embedding(input_dim = num_items, output_dim = mf_dim, name = 'mf_embedding_item', init = init_normal, W_regularizer = l2(reg_mf), input_length=1) MLP_Embedding_User = Embedding(input_dim = num_users, output_dim = layers[0]/2, name = "mlp_embedding_user", init = init_normal, W_regularizer = l2(reg_layers[0]), input_length=1) MLP_Embedding_Item = Embedding(input_dim = num_items, output_dim = layers[0]/2, name = 'mlp_embedding_item', init = init_normal, W_regularizer = l2(reg_layers[0]), input_length=1) # MF part mf_user_latent = Flatten()(MF_Embedding_User(user_input)) mf_item_latent = Flatten()(MF_Embedding_Item(item_input)) mf_vector = merge([mf_user_latent, mf_item_latent], mode = 'mul') # element-wise multiply # MLP part mlp_user_latent = Flatten()(MLP_Embedding_User(user_input)) mlp_item_latent = Flatten()(MLP_Embedding_Item(item_input)) mlp_vector = merge([mlp_user_latent, mlp_item_latent], mode = 'concat') for idx in xrange(1, num_layer): layer = Dense(layers[idx], W_regularizer= l2(reg_layers[idx]), activation='relu', name="layer%d" %idx) mlp_vector = layer(mlp_vector) # Concatenate MF and MLP parts #mf_vector = Lambda(lambda x: x * alpha)(mf_vector) #mlp_vector = Lambda(lambda x : x * (1-alpha))(mlp_vector) predict_vector = merge([mf_vector, mlp_vector], mode = 'concat') # Final prediction layer prediction = Dense(1, activation='sigmoid', init='lecun_uniform', name = "prediction")(predict_vector) model = Model(input=[user_input, item_input], output=prediction) return model
代码的前半部分分别是GMFe和MLP的内部layer构建过程,在 predict_vector = merge([mf_vector, mlp_vector], mode = 'concat')这一行开始对两者的输出进行了merge,方式为concat。最后包了一层的sigmoid。
看完了构建模型的代码,下面关注几个细节:
- 训练样本的正负比例如何设定?
def get_train_instances(train, num_negatives): user_input, item_input, labels = [],[],[] num_users = train.shape[0] for (u, i) in train.keys(): # positive instance user_input.append(u) item_input.append(i) labels.append(1) # negative instances for t in xrange(num_negatives): j = np.random.randint(num_items) while train.has_key((u, j)): j = np.random.randint(num_items) user_input.append(u) item_input.append(j) labels.append(0) return user_input, item_input, labels
该函数是获取用户和物品的训练数据,其中num_negatives控制着正负样本的比例,负样本的获取方法也简单粗暴,直接随机选取用户没有选择的其余的物品。
- 保存了训练的模型,该怎么对数据进行预测?我们从evalute.py中的源码中可以得到答案
def eval_one_rating(idx): rating = _testRatings[idx] items = _testNegatives[idx] u = rating[0] gtItem = rating[1] items.append(gtItem) # Get prediction scores map_item_score = {} users = np.full(len(items), u, dtype = 'int32') predictions = _model.predict([users, np.array(items)], batch_size=100, verbose=0) for i in xrange(len(items)): item = items[i] map_item_score[item] = predictions[i] items.pop() # Evaluate top rank list ranklist = heapq.nlargest(_K, map_item_score, key=map_item_score.get) hr = getHitRatio(ranklist, gtItem) ndcg = getNDCG(ranklist, gtItem) return (hr, ndcg)
输入只要保证和训练的时候的格式一样即可,这里作者事先构建了negative的数据,也就是说对negative的物品和测试集合中的某一个物品进行了预测,最终选取topK的,来评测是否在其中(注getHitRatio函数不是最终结果,只是0/1) eval_one_rating 函数只是对测试集合中的某个用户的某个物品,以及和事先划分好的负样本组合在一起进行预测,最终输出该测试物品是否在topK中。
- Embedding 层的物品的latent_dim和用户的latent_dim是一致的,如果不一致是否可以?在实际中未必两者的维度是一致的,这里受限于keras的merge函数的参数要求,输入的数据的shape必须是一致的,所以必须是一致的。以及Merge中的mode参数,至于什么时候选择contact,什么时候选择mul,我觉得依赖于模型效果,在实际工程中选择使得最优的方式。
python MLP.py --dataset ml-1m --epochs 20 --batch_size 256 --layers [64,32,16,8]这是运行MLP的参数,layers的参数在逐渐减小,这也是深度神经网络的潜在设置,一般意义上越深的layer是对前面的更高层次的抽象。



