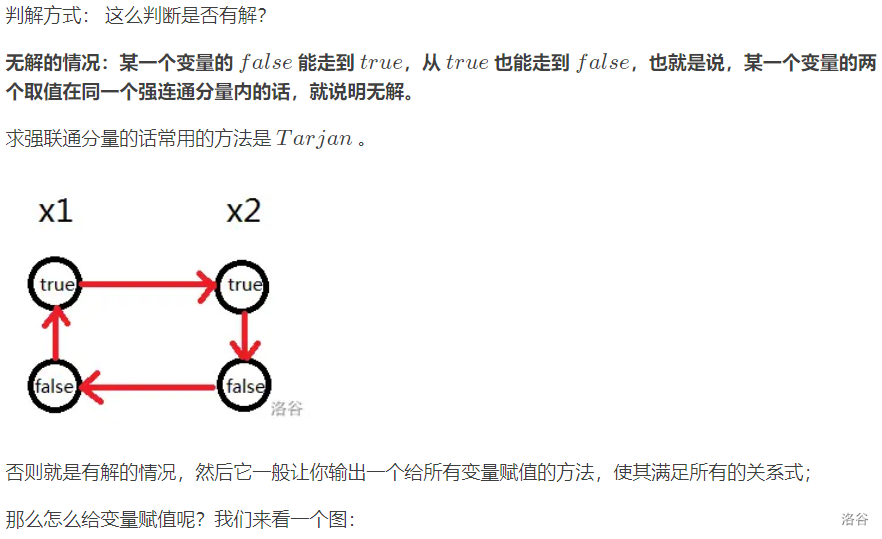
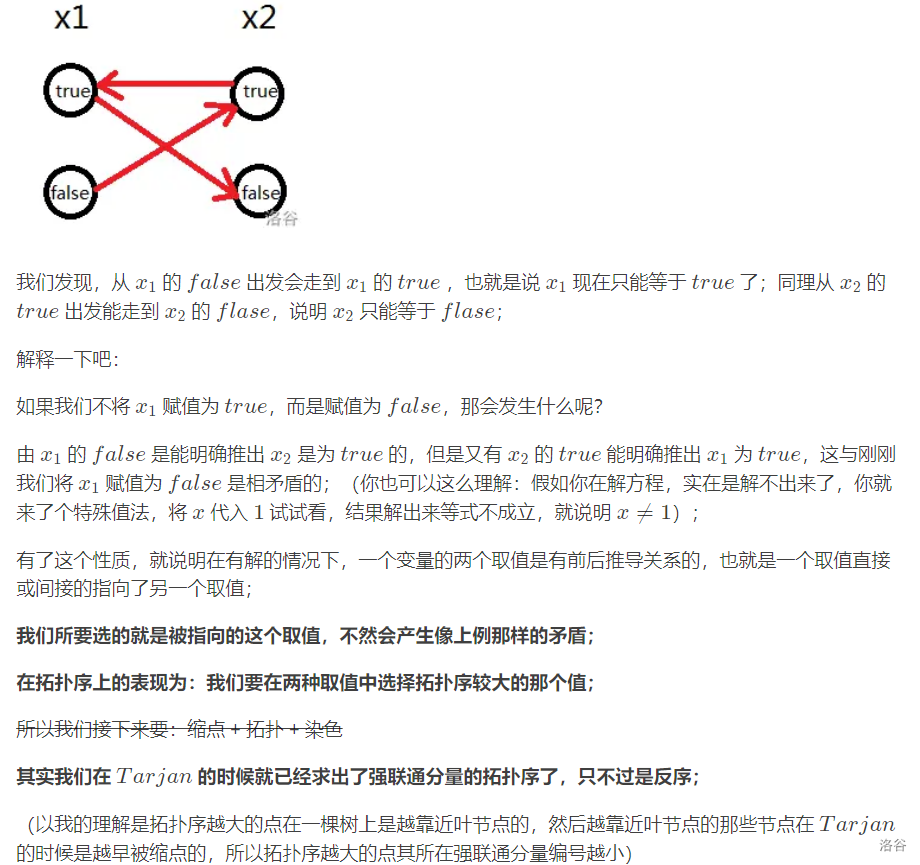
2-SAT 问题



https://www.luogu.com.cn/problem/P4782
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<vector>
using namespace std;
long long read()
{
char ch=getchar();
long long a=0,x=1;
while(ch<'0'||ch>'9')
{
if(ch=='-') x=-x;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
a=(a<<1)+(a<<3)+(ch-'0');
ch=getchar();
}
return a*x;
}
const int N=4e6+5;
int n,m,a,b,x,y,tim,top,edge_sum,scc_sum;
int dfn[N],low[N],st[N],vis[N],scc[N],head[N];
struct node
{
int to,next;
}A[N];
void add(int from,int to)
{
edge_sum++;
A[edge_sum].next=head[from];
A[edge_sum].to=to;
head[from]=edge_sum;
}
void tarjan(int u)
{
dfn[u]=low[u]=++tim;
st[++top]=u;
vis[u]=1;
for(int i=head[u];i;i=A[i].next)
{
int v=A[i].to;
if(!dfn[v])
{
tarjan(v);
low[u]=min(low[u],low[v]);
}
else if(vis[v]) low[u]=min(low[u],dfn[v]);
}
if(dfn[u]==low[u])
{
scc_sum++;
while(st[top]!=u)
{
scc[st[top]]=scc_sum;
vis[st[top]]=0;
top--;
}
scc[st[top]]=scc_sum;
vis[st[top]]=0;
top--;
}
}
int main()
{
n=read();m=read();
for(int i=1;i<=m;i++)
{
a=read();x=read(); //第a个数为x或第b个数为y
b=read();y=read();
if(x==0&&y==0) //"如果第a个数为0或第b个数为0"至少满足其一
{
add(a+n,b); //a=1则b=0
add(b+n,a); //b=1则a=0
}
if(x==0&&y==1) //"如果第a个数为0或第b个数为1"至少满足其一
{
add(a+n,b+n); //a=1则b=1
add(b,a); //b=0则a=0
}
if(x==1&&y==0) //"如果第a个数为1或第b个数为0"至少满足其一
{
add(a,b); //a=0则b=0
add(b+n,a+n); //b=1则a=1
}
if(x==1&&y==1) //"如果第a个数为1或第b个数为1"至少满足其一
{
add(a,b+n); //a=0则b=1
add(b,a+n); //b=0则a=1
}
}
for(int i=1;i<=2*n;i++) //对每个变量的每种取值进行tarjan
{
if(!dfn[i]) tarjan(i);
}
for(int i=1;i<=n;i++) //判断无解的情况
{
if(scc[i]==scc[i+n]) //同一变量的两种取值在同一强联通分量里,说明无解
{
printf("IMPOSSIBLE\n");
return 0;
}
}
printf("POSSIBLE\n"); //否则就是有解
for(int i=1;i<=n;i++)
{
if(scc[i]>scc[i+n]) printf("1 "); //强联通分量编号越小 -> 拓扑序越大 -> 越优
else printf("0 ");
}
return 0;
}
P4171 [JSOI2010] 满汉全席
https://www.luogu.com.cn/problem/P4171
分析:非常典型的一道2——SAT问题
将满式(m)看做取0 汉式(h)看做取1 例如h1表示X1=1,m3表示X3=0
这样按照模板建边跑Tarjan即可 最后判断每个位置Xi的true点和false点是否在同一个联通快内
如果在的话 表示不可能 所有位置都不在的话 表示可能
#include<bits/stdc++.h>
using namespace std;
const int N=1e4;
int n,m,a,b,x,y,tim,top,edge_sum,scc_sum;
int dfn[N],low[N],st[N],vis[N],scc[N],head[N];
struct node
{
int to,next;
}A[N];
void add(int from,int to)
{
edge_sum++;
A[edge_sum].next=head[from];
A[edge_sum].to=to;
head[from]=edge_sum;
}
void tarjan(int u)
{
dfn[u]=low[u]=++tim;
st[++top]=u;
vis[u]=1;
for(int i=head[u];i;i=A[i].next)
{
int v=A[i].to;
if(!dfn[v])
{
tarjan(v);
low[u]=min(low[u],low[v]);
}
else if(vis[v]) low[u]=min(low[u],dfn[v]);
}
if(dfn[u]==low[u])
{
scc_sum++;
while(st[top]!=u)
{
scc[st[top]]=scc_sum;
vis[st[top]]=0;
top--;
}
scc[st[top]]=scc_sum;
vis[st[top]]=0;
top--;
}
}
void init(){
edge_sum=tim=scc_sum=0;
memset(head,0,sizeof(head));
memset(dfn,0,sizeof(dfn));
memset(vis,0,sizeof(vis));
memset(scc,0,sizeof(scc));
memset(low,0,sizeof(low));
}
void solve(){
init();
cin>>n>>m;
for(int i=1;i<=m;i++)
{
char c1,c2;
int x,y,a,b;
cin>>c1>>a>>c2>>b;
if(c1=='h')x=1;
else x=0;
if(c2=='h')y=1;
else y=0;
if(x==0&&y==0)add(a+n,b),add(b+n,a);
if(x==0&&y==1)add(a+n,b+n),add(b,a);
if(x==1&&y==0)add(a,b),add(b+n,a+n);
if(x==1&&y==1)add(a,b+n),add(b,a+n);
}
for(int i=1;i<=2*n;i++)
if(!dfn[i]) tarjan(i);
for(int i=1;i<=n;i++)
if(scc[i]==scc[i+n])
{
printf("BAD\n");
return ;
}
printf("GOOD\n");
}
int main()
{
int T;cin>>T;
while(T--)solve();
return 0;
}



