牛客挑战赛67
A 构造

分析:

这个题目思维挺好的
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int M=1000005;
int p[M];
int main()
{
int n,a,b,t;
cin>>t;
while(t--)
{
cin>>n>>a>>b;
p[a]=b;
if(a<=n&&b<=n||a>n&&b>n)
{
for(int i=1;i<=n*2;i++) p[i]=i;
swap(p[a],p[b]);
}
else
{
for(int i=n*2;i>=1;i--) p[n*2+1-i]=i;
swap(p[a],p[n*2+1-b]);
}
for(int i=1;i<=n*2;i++) printf("%d ",p[i]);
cout<<endl;
}
return 0;
}
B数据结构
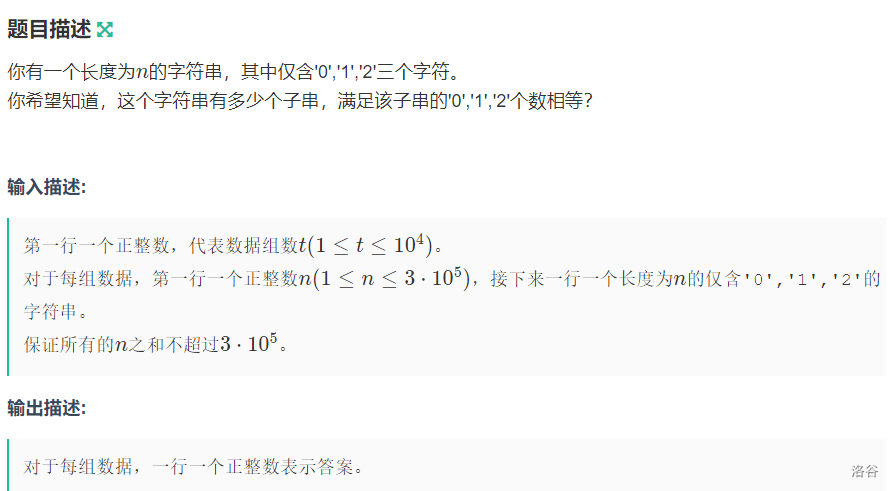
分析:
考虑如果只考虑01 这样只需要搞个前缀和加map即可统计
现在还需要满足2的个数与01也需相同
一个朴素的想法是将01个数相同的区间存下来 然后判断区间2的个数是否和01的相同
但是毫无疑问 答案区间个数可能是超int的 这样不行 那怎么办呢
考虑统计01前缀的时候顺便也统计2即可 再维护pre1[i]-pre2[i]
表示前缀1与2的差值 找的时候如果前面有pre1[j]-pre2[j]的值和当前pre1[i]-pre2[i]的值相同
也就是 pre1[j]-pre2[j]=pre1[i]-pre[i] 左右交换一下 pre1[i]-pre1[j]=pre2[i]-pre2[j] 就是1和2的数量相同
#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define ll long long
void solve();
const int maxn=3e5+5;
int n;
ll ans;
map<pair<int,int>,int>mp;
int a[maxn],pre2[maxn],pre1[maxn],pre[maxn];
int main(){
int T;cin>>T;
while(T--)solve();
return 0;
}
void solve(){
cin>>n;
ans=0;
pair<int,int>t;
pre2[0]=pre[0]=pre1[0]=0;
mp.clear();
t.first=0,t.second=0;
mp[t]++;
for(int i=1;i<=n;i++){
scanf("%1d",&a[i]);
if(a[i]==0)a[i]=-1;
pre1[i]=pre1[i-1]+(a[i]==1);
pre2[i]=pre2[i-1]+(a[i]==2);
if(a[i]==-1)
pre[i]=pre[i-1]-1;
else if(a[i]==1)pre[i]=pre[i-1]+1;
else pre[i]=pre[i-1];
t.first=pre[i],t.second=pre1[i]-pre2[i];
ans+=mp[t];
mp[t]++;
}
cout<<ans<<endl;
}
C 点分治

分析:

这个题目巧妙的地方就是在于 设置了深度为d 最大子树为s 这样只需要二分找到满足子树最小要求的最大深度即可
#include<bits/stdc++.h>
using namespace std;
int t;
int n;
long long k;
vector<int>G[200010];
int mson[200010],siz[200010],dep[200010],mxd[200010];
int mx[200010];
int ans;
void dfs1(int x,int p)
{
mson[x]=0;
siz[x]=1;
mxd[x]=dep[x];
long long res=1;
for(int i=0;i<(int)G[x].size();i++)
{
int y=G[x][i];
if(y==p)continue;
dep[y]=dep[x]+1;
dfs1(y,x);
mxd[x]=max(mxd[x],mxd[y]);
res+=1LL*siz[x]*siz[y];
siz[x]+=siz[y];
if(!mson[x] || siz[y]>siz[mson[x]])mson[x]=y;
}
res+=1LL*siz[x]*(n-siz[x]);
if(res>=k)ans=max(ans,1);
}
void calc(int x,int p,int t,int tt)
{
long long nd=(k+siz[x]-1)/siz[x];
if(mx[dep[t]+1]>=nd)
{
int l=dep[t]+1,r=mxd[t]+1;
while(l+1<r)
{
int mid=(l+r)>>1;
if(mx[mid]<nd)r=mid;else l=mid;
}
ans=max(ans,l+dep[x]-dep[t]-dep[t]+1);
}
if(1LL*siz[x]*(n-siz[tt])>=k)ans=max(ans,dep[x]-dep[t]+1);
for(int i=0;i<(int)G[x].size();i++)
{
int y=G[x][i];
if(y==p)continue;
calc(y,x,t,tt);
}
}
void update(int x,int p)
{
mx[dep[x]]=max(mx[dep[x]],siz[x]);
for(int i=0;i<(int)G[x].size();i++)
{
int y=G[x][i];
if(y==p)continue;
update(y,x);
}
}
void del(int x,int fa){
mx[dep[x]]=0;
for(int i=0;i<G[x].size();i++)
if(G[x][i]!=fa)del(G[x][i],x);
}
void dfs2(int x,int p)
{
for(int i=0;i<(int)G[x].size();i++)
{
int y=G[x][i];
if(y==p || y==mson[x])continue;
dfs2(y,x),del(y,x);
}
if(mson[x])
{
dfs2(mson[x],x);
long long nd=(k+n-siz[mson[x]]-1)/(n-siz[mson[x]]);
if(siz[mson[x]]>=nd)
{
int l=dep[x]+1,r=mxd[mson[x]]+1;
while(l+1<r)
{
int mid=(l+r)>>1;
if(mx[mid]<nd)r=mid;else l=mid;
}
ans=max(ans,l-dep[x]+1);
}
}
for(int i=0;i<(int)G[x].size();i++)
{
int y=G[x][i];
if(y==p || y==mson[x])continue;
calc(y,x,x,y);
update(y,x);
}
mx[dep[x]]=max(mx[dep[x]],siz[x]);
}
int main()
{
scanf("%d",&t);
while(t--)
{
scanf("%d%lld",&n,&k);
for(int i=1;i<=n;i++)G[i].clear();
for(int i=1;i<n;i++)
{
int u,v;
scanf("%d%d",&u,&v);
G[u].push_back(v);
G[v].push_back(u);
}
ans=0;
dfs1(1,0);
dfs2(1,0),del(1,0);
printf("%d\n",ans);
}
return 0;
}


