2022牛客国庆集训派对day1

B

题意：

给定一个01字符串，你需要找到最长的一个子串和最长的一个子序列，分别使得其中01的个数相同。

做法：

子序列很好算 2×min(cnt0,cnt1)

子串可以考虑前缀和

将0与1的个数差前缀和 每次询问当前的前缀和x 如果之前出现前缀和为y 使得x+y=0即成立

最后取个最大值就好

void solve() {
    int n; cin >> n;
    string s; cin >> s;
    s = " " + s;
    int ans = 0, cnt = 0;
    map<int,int> mp;
    mp[0] = 0;
    for (int i = 1; i <= n; i++) {
        if (s[i] == '1') cnt++;
        else cnt--;
        if(mp.count(cnt)) ans = max(ans, i - mp[cnt]);
        else mp[cnt] = i;
    }
    cout << ans << " ";
    int cnt1 = 0, cnt0 = 0;
    for (int i = 1; i <= n; i++) {
        if (s[i] == '0') cnt0++;
        else cnt1++;
    }
    cout << min(cnt1, cnt0) * 2 << endl;
}

很神奇的做法：

假设开始线是水平的 然后我们可以找到第一条使得过线和线上方的点大于总点数的线

然后使得这条线倾斜一丢丢就好

map<int, vector<int>>mp;
int n;
void slove() {
    cin >> n;
    mp.clear();
    for (int i = 1; i <= n; i++) {
        int x, y;
        cin >> x >> y;
        mp[y].push_back(x);
    }
    int pre = 0;
    for (auto p : mp) {
        sort(p.second.begin(), p.second.end());
        pre += p.second.size();
        if (pre >= n / 2) {
            pre -= p.second.size();
            for (int x : p.second) {
                pre++;
                if (pre == n / 2) {//找到中间点
                    //x   y 
                    int y = p.first;
                    cout << int(x + 1e8) + 1<<" " << y - 1 << " " << int(x - 1e8) <<" " << y + 1 << endl;
                    break;
                }
            }
            break;
        }
    }    
}

G

题意：

给你n个数，问你有多少个长度不小于2的连续子序列，使得其中最大元素不大于所有元素和的一半。

做法

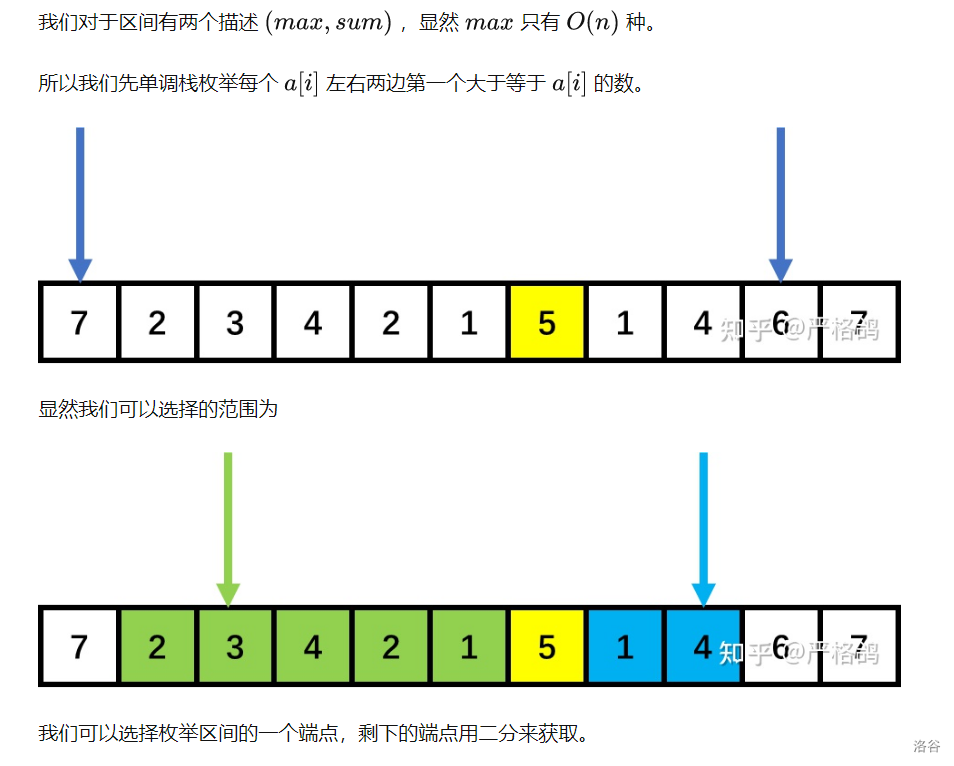
还是用到容斥原理

int a[N], n, pre[N];
int sum(int L, int R) {
    if (L > R)return 0;
    return pre[R] - pre[L - 1];
}
int LL[N], RR[N];
void slove() {
    cin >> n;
    for (int i = 1; i <= n; i++)cin >> a[i];
    for (int i = 1; i <= n; i++)pre[i] = pre[i - 1] + a[i];
    a[0] = 1e18, a[n + 1] = 1e18;
    stack<int>stk; stk.push(0);
    for (int i = 1; i <= n; i++) {
        while (a[stk.top()] < a[i])stk.pop();
        LL[i] = stk.top();
        stk.push(i);
    }
    while (stk.size())stk.pop();
    stk.push(n + 1);
    for (int i = n; i >= 1; i--) {
        while (a[stk.top()] < a[i])stk.pop();
        RR[i] = stk.top();
        stk.push(i);
    }
    int ans = 0;
    for (int i = 1; i <= n; i++) {
        int L_len = i - LL[i], R_len = RR[i] - i;
        if (L_len <= R_len) {
            int mx = a[i];
            for (int j = LL[i] + 1; j <= i; j++) {
                auto k = lower_bound(pre + i, pre + RR[i], 2 * mx + pre[j - 1]) - pre;
                ans += (k - i);
            }
        }
        else {
            int mx = a[i];
            for (int j = i; j < RR[i]; j++) {
                auto k = lower_bound(pre + LL[i], pre + i, pre[j] - 2 * mx + 1) - pre;
                ans += i - k;
            }
        }
    }
    cout << n * (n + 1) / 2 - ans << endl;
}