2022杭电多校4
1004 Link with Equilateral Triangle
题意:给一个边长为n的大等边三角形,含有n2个边长为1的小等边三角形,在每个小等边三角形的顶点上填数字(0或1或2),大等边三角形的左侧不能填0,右侧不能填1,底部不能填2,且每个小三角形三个顶点上的数加起来不能是3的倍数。
找规律,我们发现无论n是多少都无法满足要求,直接输出No就行了。
#include<bits/stdc++.h>
using namespace std;
void solve() {
int n;
cin >> n;
cout << "No\n";
}
int main() {
int t;
cin >> t;
while(t--)
solve();
return 0;
}
1006 BIT Subway
题意:本月买票花费大于等于100后,以后的票8折;大于等于200后,以后的票5折。
DLee认为一张票的价格可以分成两部分买,比如:
本月已经花费了199元,接下来买10元和8元的票可以这么买199 + 1.25 * 0.8 + 8.75 * 0.5 + 8 * 0.5 = 208.375
实际上,可以分成不止两部分。
#include<bits/stdc++.h>
using namespace std;
void solve(){
int n;
scanf("%d", &n);
double pre = 0, cur = 0, sum = 0, x;
//pre是拆分买票,cur是不拆分买票。
for(int i = 1; i <= n; i++){
scanf("%lf", &x);
if(cur >= 200) cur += x * 0.5;
else if(cur >= 100) cur += x * 0.8;
else cur += x;
sum += x;
}
if(sum > 100){
pre = 100;
sum -= 100;
if(sum * 0.8 > 100){
sum -= 125; //125元打8折刚好是100元
pre = 200;
pre += sum * 0.5;
}else pre += sum * 0.8;
}else pre = sum;
printf("%.3lf %.3lf\n", pre, cur);
}
int main() {
int T;
scanf("%d", &T);
while(T--)
solve();
return 0;
}
1007 Climb Stairs
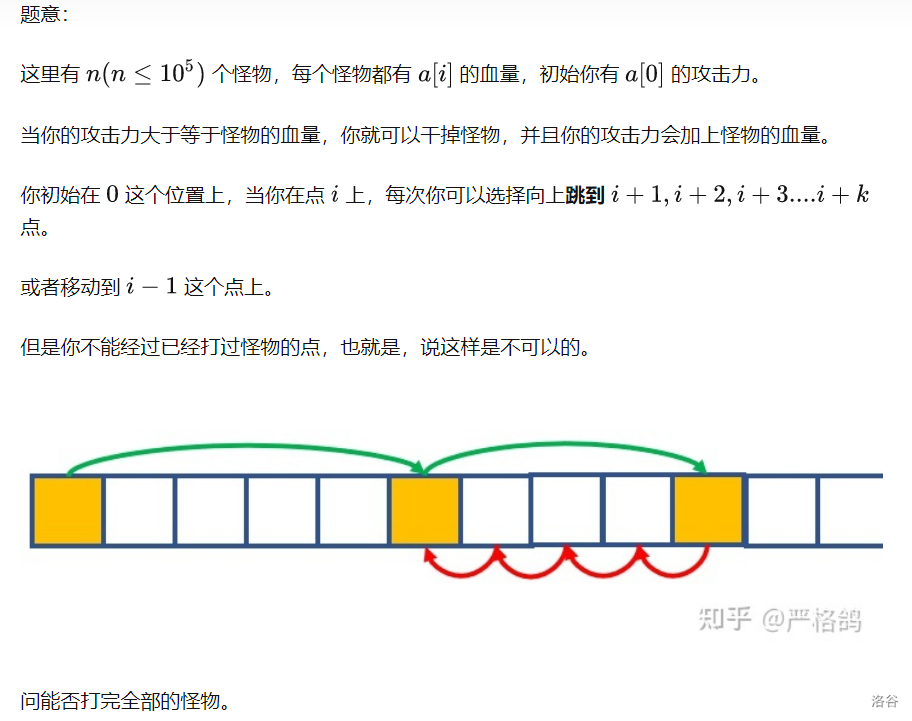
贪心,暴力。
由于我们可以往上跳几层楼,但是只能一层一层下来且去过的楼层不能再去,因此我们只需要贪心的找我们能跳的最近的点就行了。
首先我们使用前缀和处理出怪物的血量,这样我们跳的时候可以快速得到经过楼层的怪物血量的和。
其次我们用p数组记录下跳到第i个位置且能一直往下走所需要的最低攻击力。
得到这两个数组之后暴力的找到能跳的最近的点,然后一直往下层走,走到底然后重复这个操作,如果在k层以内找不到能跳的点,就输出NO,如果找到能跳的点为n,输出YES。
#include<bits/stdc++.h>
const int N = 1e5 + 5;
using namespace std;
int n, m, k, t, T;
long long a[N], sum[N], p[N];
void solve(){
long long m;
cin >> n >> m >> k;
for(int i = 1; i <= n; i++){
cin >> a[i];
sum[i] = sum[i - 1] + a[i];
p[i] = max(p[i - 1] - a[i], a[i]);
}
int pos = 0;//能跳的最近的位置
int loc = 0;//当前的位置
int f = 1;
while(1){
int mii = -1;//记录能跳的最近的点
for(int i = pos + 1; i <= loc + k && i <= n; i++){//枚举能跳的所有楼层,找最近的
if(m >= max(p[i - 1] - a[i], a[i])){
mii = i;
break;
}
}
if(mii == -1){
f = 0;
break;
}
p[mii] = 0;
m += sum[mii] - sum[pos];//加上经过楼层的怪物血量的和
loc = pos + 1;//因为跳上去之后我们要往下走回来,所以应该是上一次最近的点+1
pos = mii;
if(pos == n){
f = 1;
break;
}
}
if(f) cout << "YES\n";
else cout << "NO\n";
}
int main(){
cin >> T;
while(T--)
solve();
return 0;
}
1011 Link is as bear
题意:有长度有n的数组,Link每次能选择区间[l, r]让其中的数都变成[l, r]中所有数的异或和,求最后让数组所有的数都变成一样的数的最大值。
假设我们选择数组中的某一些不连续的数异或起来是最后的答案,那么我们只需要对每个断层进行两次操作就可以让其中的断层都变成0,而任何数异或0都是本身。
考虑线性基,直接求出数组中某一些数的异或最大值就是答案了。模板题啊
#include<bits/stdc++.h>
#define LL long long
using namespace std;
int n, m, k, t, T;
LL b[64];
void insert(LL x){
for(int i = 63; i >= 0; i--)
if(x & (1ll << i))
if(b[i]) x ^= b[i];
else{
b[i] = x;
break;
}
}
void get_mx(){
LL ans = 0;
for(int i = 63; i >= 0; i--)
ans = max(ans, ans ^ b[i]);
printf("%lld\n", ans);
}
void solve(){
scanf("%d", &n);
LL x;
for(int i = 1; i <= n; i++){
scanf("%lld", &x);
insert(x);
}
get_mx();
}
int main(){
scanf("%d", &T);
while(T--)
solve();
return 0;
}
A 1001 Link with Bracket Sequence II
题意:给定一个长度为n的数组,若a[i] == 0,那么表示这个位置填入的括号未知,若|a[i]|> 0 表示这个位置填入第|a[i]|种括号,左括号为正,右括号为负,求填满这个括号序列的方案数。
分析:n <= 500,因此我们考虑区间dp。对于所有括号序列,我们从两种情况进行转移,f[l][r]表示对于一个从范围为[l, r]的合法括号序列,且l和r处的括号序列位置相匹配的方案数。g[l][r]表示[l, r]的合法括号序列的方案数。
为什么要这么设定呢?因为括号的种类有m种,我们如何用这个m呢?就是枚举到两端均是0的时候直接可以乘一个m,但是这只是对于f来说的转移方程。而g是更加普遍的情况,如何转移呢?我们考虑区间分点,g[l][r]种找到一个分界线k,那么可以得出转移方程:g[l][r] += g[l][k - 1] * f[k][r]。这个堆叠方向是人为规定的,是为了避免重复计数。
其实只要想清楚如何防止重复统计就可以,我们一般都认为定义一种转移方式,转移方式有许多,比如这道题我们的g是从g+f的方式转移,这样恰好能够不重不漏计算出所有满足要求的g。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <set>
#include <vector>
#include <cmath>
using namespace std;
typedef long long ll;
#define int long long
#define NO {puts("NO") ; return ;}
#define YES {puts("YES") ; return ;}
#define please return
#define ac 0
typedef pair<int, int> PII;
const int N = 510 , INF = 0x3f3f3f3f , mod = 1e9 + 7;
int n, m, a[N];
int f[N][N], g[N][N];
void solve()
{
cin >> n >> m;
for(int i = 1 ; i <= n ; i ++ ) cin >> a[i];
memset(f, 0, sizeof f);
memset(g, 0, sizeof g);
if(n & 1)
{
puts("0");
return ;
}
for(int i = 0 ; i <= n ; i ++ )
g[i + 1][i] = 1;
for(int len = 2 ; len <= n ; len += 2)
for(int l = 1 ; l + len - 1 <= n ; l ++ )
{
int r = l + len - 1;
if(a[l] >= 0 && a[r] <= 0)
{
int t = 0;
if(a[l] == 0 && a[r] == 0) t = m;
else if(a[l] == 0 || a[r] == 0) t = 1;
else if(a[l] + a[r] == 0) t = 1;
else t = 0;
f[l][r] = g[l + 1][r - 1] * t % mod;
}
for(int k = l ; k <= r ; k += 2)
g[l][r] = (g[l][r] + g[l][k - 1] * f[k][r] % mod) % mod;
}
cout << g[1][n] << endl;
}
signed main()
{
ios::sync_with_stdio(0),cin.tie(0);
int T = 1;
cin >> T;
while(T -- ) solve();
please ac;
}
实际上不用设f数组的 直接从g[l+1][r-1]×t转移就好
因为是区间dp 初始化还是很重要的g[i+1][i]=1 看转移方程如果k-1比L小的时候就应该取1 !!!!!!!!
1003 Magic

好久没有碰到差分约束的题目了
#include <bits/stdc++.h>
using namespace std;
using T = pair<int, int>;
const int N = 10010;
int n, k; // 长度和范围
vector<T> g[N];
int dist[N], cnt[N];
bool inq[N];
void addEdge (int u, int v, int w) {
g[u].push_back({v, w});
}
void init () {
for (int i = 0; i <= n; i ++ ) g[i].clear();
memset(cnt, 0, sizeof cnt);
memset(inq, 0, sizeof inq);
}
int spfa () {
queue<int> q;
memset(dist, -0x3f, sizeof dist);
dist[0] = 0;
q.push(0); inq[0] = true;
while(!q.empty()) {
int u = q.front(); q.pop();
inq[u] = false;
++ cnt[u];
if (cnt[u] > 2 * n) return -1;
for (T edge: g[u]) {
int v = edge.first, d = edge.second;
if (dist[v] < dist[u] + d) {
dist[v] = dist[u] + d;
if (!inq[v]) {
q.push(v); inq[v] = true;
}
}
}
}
return dist[n] == -0x3f3f3f3f ? -1 : dist[n];
}
void solve () {
init();
scanf("%d%d", &n, &k);
for (int i = 1; i <= n; i ++ ) {
int pi; scanf("%d", &pi);
addEdge(max(0, i - k), min(n, i + k - 1), pi);
}
int q; scanf("%d", &q);
while(q -- ) {
int l, r, b; scanf("%d%d%d", &l, &r, &b);
addEdge(r, l - 1, -b);
}
for (int i = 1; i <= n; i ++ ) addEdge(i - 1, i, 0);
printf("%d\n", spfa());
}
int main () {
int ts; scanf("%d", &ts); while(ts -- ) solve();
return 0;
}





