山东大学(威海)2022多校结训赛

A 多

首先题意要理解清楚 操作是按照顺序来的 直接dp即可

dp[i]表示当前将坏电脑停在i位置最少不执行的条数

设(u,v) 设A=dis[u]，B=dis[v]

转移：

dis[u]=min(A+1,B)使得坏电脑要保存在当前位置该条操作应该不执行

同理 dis[v]=min(A,B+1)

为什么要设A和B？ 因为避免第一次转移的时候影响到第二次转移

执行或者不执行是两个并列的

#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define ll long long
const int maxn=1e5+5;
int n,m,k;
int dis[maxn];
int main(){
	int T;
	cin>>T;
	while(T--){
		memset(dis,0x7f,sizeof(dis));
		scanf("%d%d%d",&n,&m,&k);
		dis[k]=0;
		for(int i=1;i<=m;i++){
			int uu,vv;
			scanf("%d%d",&uu,&vv);
			int U=dis[uu],V=dis[vv];
			dis[uu]=min(U+1,V);
			dis[vv]=min(V+1,U);
		}
		for(int i=1;i<=n;i++)
		if(dis[i]!=2139062143)
		printf("%d ",dis[i]);
		else printf("-1 ");
        cout<<endl;
	}
     return 0;
}

D 训

分析：

发现正着推插入操作会有跳跃 但是如果逆着推就不会跳跃 而是在整个整体左右进行插入操作

所以直接倒着推 用deque模拟插入操作即可

#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define ll long long
int main(){
	int n;
	cin>>n;
	string s;
	cin>>s;
	int len=s.size();
	deque<int>q;
	q.push_front(len);
	for(int i=len-1;i>=0;i--){
		int id=i;
		if(s[i]=='L'){
			q.push_back(i);
		}else{
			q.push_front(i);
		}
	}
	while(!q.empty()){
		printf("%d ",q.front());
		q.pop_front();
	}
     return 0;
}

F 最大权重

这个题真的够极限的 最后十分钟想出来了 当时连正确性都没法保证 一遍交就过了

很容易想到考虑每条边的贡献 因为是最大边权 所以想到排序 从小到大处理 (因为要先处理小的边 后处理大的边跟新当前最大值)

考虑并查集

设一条边(u,v) 边权为w。如果u，v不在一个集合里面，那么w就为u集合里面的点到v集合里面大的点的最大边权

如果u，v已经在一个集合里面 这种情况实际上是不可能的 这样就形成一个环了 不成立

#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define ll long long
const int maxn=1e5+5;
ll fa[maxn],sz[maxn];
int n;
int cnt;
ll ans;
struct node{
	int a,b;ll w;
}edg[maxn];
bool cmp(node aa,node bb){
	return aa.w<bb.w;
}
int find(int x){
	if(fa[x]!=x)return fa[x]=find(fa[x]);
	return x;
}
int main(){
	cin>>n;
	for(int i=1;i<n;i++)
		scanf("%d%d%lld",&edg[i].a,&edg[i].b,&edg[i].w);
	for(int i=1;i<=n;i++)fa[i]=i,sz[i]=1;
	sort(edg+1,edg+n,cmp);
	for(int i=1;i<n;i++){
		int uu=edg[i].a,vv=edg[i].b;
		ll ww=edg[i].w;
		int fu=find(uu),fv=find(vv);
		if(fu!=fv){
			ans+=sz[fu]*sz[fv]*ww;
			fa[fu]=fv;
			sz[fv]+=sz[fu];
		}
	}
	cout<<ans;
     return 0;
}

B 贪吃蛇

两点之间一定是曼哈顿距离最短 关键在于考虑当时贪吃蛇的方向

分情况讨论就好了 4×4=16种情况

#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define ll long long
int T; 
int x,y,d,n;
void solve();
int main(){
	cin>>T;
	while(T--)
	solve();
     return 0;
}
void solve(){
	string s="";
	scanf("%d%d%d%d",&x,&y,&d,&n);
	for(int i=1;i<=n;i++){
		int xx,yy;
		scanf("%d%d",&xx,&yy);
		if(x<=xx&&yy>=y){
			if(d==0){
				for(int j=1;j<=(yy-y);j++)s+='f';
				s+='c';
				for(int j=1;j<=(xx-x);j++)s+='f';
			    d=1,x=xx,y=yy;
			}
			else if(d==1){
				for(int j=1;j<=(xx-x);j++)s+='f';
			    s+='u';
			    for(int j=1;j<=(yy-y);j++)s+='f';
			    d=0,x=xx,y=yy;
			}
			else if(d==2){
				s+='u';
				for(int j=1;j<=(xx-x);j++)s+='f';
			    s+='u';
			    for(int j=1;j<=(yy-y);j++)s+='f';
			    d=0,x=xx,y=yy;
			}
			else if(d==3){
				s+='c';
				for(int j=1;j<=(yy-y);j++)s+='f';
				s+='c';
				for(int j=1;j<=(xx-x);j++)s+='f';
			    d=1,x=xx,y=yy;
			}
		}
		else if(x>=xx&&y>=yy){
			if(d==3){
				for(int j=1;j<=(x-xx);j++)s+='f';
				s+='u';
				for(int j=1;j<=(y-yy);j++)s+='f';
				d=2,x=xx,y=yy;
			}
			else if(d==2){
				for(int j=1;j<=(y-yy);j++)s+='f';
				s+='c';
				for(int j=1;j<=(x-xx);j++)s+='f';
				d=3,x=xx,y=yy;
			}
			else if(d==1){
				s+='c';
				for(int j=1;j<=(y-yy);j++)s+='f';
				s+='c';
				for(int j=1;j<=(x-xx);j++)s+='f';
				d=3,x=xx,y=yy;
			}
			else if(d==0){
				s+='u';
				for(int j=1;j<=(x-xx);j++)s+='f';
				s+='u';
				for(int j=1;j<=(y-yy);j++)s+='f';
				d=2,x=xx,y=yy;
			} 
		}
		else if(xx<=x&&y<=yy){
			if(d==0){
				for(int j=1;j<=(yy-y);j++)s+='f';
				s+='u';
				for(int j=1;j<=(x-xx);j++)s+='f';
				d=3;x=xx,y=yy;
			}
			else if(d==3){
				for(int j=1;j<=(x-xx);j++)s+='f';
				s+='c';
				for(int j=1;j<=(yy-y);j++)s+='f';
				d=0,x=xx,y=yy;
			}
			else if(d==1){
				s+='u';
				for(int j=1;j<=(yy-y);j++)s+='f';
				s+='u';
				for(int j=1;j<=(x-xx);j++)s+='f';
				d=3;x=xx,y=yy;
			}
			else if(d==2){
				s+='c';
				for(int j=1;j<=(x-xx);j++)s+='f';
				s+='c';
				for(int j=1;j<=(yy-y);j++)s+='f';
				d=0,x=xx,y=yy;
			}
		}
		else if(x<=xx&&y>=yy){
			if(d==1){
				for(int j=1;j<=(xx-x);j++)s+='f';
				s+='c';
				for(int j=1;j<=(y-yy);j++)s+='f';
				d=2,x=xx,y=yy;
			}
			else if(d==2){
				for(int j=1;j<=(y-yy);j++)s+='f';
				s+='u';
				for(int j=1;j<=(xx-x);j++)s+='f';
				d=1,x=xx,y=yy;
			}
			else if(d==3){
				s+='u';
				for(int j=1;j<=(y-yy);j++)s+='f';
				s+='u';
				for(int j=1;j<=(xx-x);j++)s+='f';
				d=1,x=xx,y=yy;
			}
			else if(d==0){
				s+='c';
				for(int j=1;j<=(xx-x);j++)s+='f';
				s+='c';
				for(int j=1;j<=(y-yy);j++)s+='f';
				d=2,x=xx,y=yy;
			}
		}
	}
	cout<<s<<endl;
}

A 立方体

思路 ：由题意知，要求等边三角形的数量，每个立方体有八个顶点，所以有8个等边三角形。等价于求立方体的数量。

注意两数相乘超出longlong范围了 要么用int_128 要么用快速幂！！！

    #include<bits/stdc++.h>
    using namespace std;
    #define lowbit(x) x&(-x)
    #define ll long long
    const int mod=1e9+7;
    ll fast_mi(ll aa,ll bb){
        ll res=1;
        while(bb){
            if(bb&1)res=res*aa%mod;
            aa=aa*aa%mod;
            bb>>=1;
        }
        return res;
    }
    int main(){
        int T;
        cin>>T;
        while(T--){
            ll n;
            scanf("%lld",&n);
            cout<<fast_mi((n-1)%mod,2)*fast_mi(n%mod,2)%mod*2%mod<<endl;
        }
         return 0;
    }

总结一下几个公式：

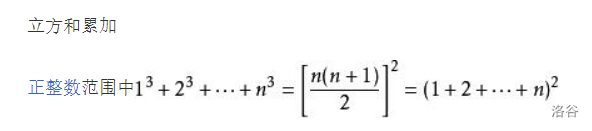
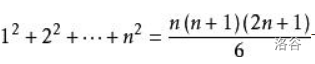
E 添加方向