"蔚来杯"2022牛客暑期多校训练营2
J题
Link with Arithmetic Progression


以上相当于最小二乘法的推导过程
要求具体的值话 还是要用到高中大题里面的公式

这个题得出来 其实等差数列就是一个线性函数上的点
#include <stdio.h>
const int N=1e5+7;
int s[N];
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
int n;
double sum=0,x,y,sum1=0,sum2=0,a,b,ans=0;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&s[i]);
sum+=s[i];
}
x=(n+1)/2.0;y=sum/n;
for(int i=1;i<=n;i++)
{
sum1+=(x-i)*(x-i);
sum2+=(x-i)*(y-s[i]);
}
b=sum2/sum1;a=y-b*x;
for(int i=1;i<=n;i++)
ans+=(s[i]-b*i-a)*(s[i]-b*i-a);
printf("%.10lf\n",ans);
}
return 0;
}
G题
Link with Monotonic Subsequence
题意: 构造长度为n的排列P 使得max(lis(P),lds(P))最小
开始一直不知道怎么构造 后面构造出了 321 654 987 这样的序列
就发现其实可以sqrt(n)分块构造 这样一定是最优的
#include<bits/stdc++.h>
using namespace std;
int main (){
int T;
cin>>T;
while(T--){
int n;
scanf("%d",&n);
int k=sqrt(n);
int re=n-k*k;
if(re!=0)k++,re=n-n/k*k;
for(int i=1;i<=n/k;i++)
for(int j=i*k;j>=i*k-k+1;j--)
printf("%d ",j);
for(int i=1;i<=re;i++)
printf("%d ",n-i+1);
printf("\n");
}
return 0;
}
K题
Link with Bracket Sequence I
比赛的时候发现一会就有好多人做出来了 但是想了半天还是不会做
题意:
已知括号序列a是一个长度为n的合法括号序列b的子序列,求可能的序列b的数量。

#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define ll long long
const int maxn=205;
const int mod=1e9+7;
int T,n,m;
string s;
ll dp[maxn][maxn][maxn];
void solve();
int main(){
cin>>T;
while(T--)solve();
return 0;
}
void solve() {
cin >> n >> m;
cin >> s; s = "?" + s + "?";
for (int i = 0; i <= m; i++)for (int j = 0; j <= n; j++)for (int k = 0; k <= m; k++)dp[i][j][k] = 0;
dp[0][0][0] = 1;
for (int i = 1; i <= m; i++) {
for (int j = 0; j <= n; j++) {
for (int k = 0; k <= m; k++) {
// b 的 第i位 放 (
(dp[i][j + (s[j + 1] == '(')][k + 1] += dp[i - 1][j][k]) %= mod;
// b 的 第i位 放 )
if (k) (dp[i][j + (s[j + 1] == ')')][k - 1] += dp[i - 1][j][k]) %= mod;
}
}
}
cout << dp[m][n][0] << endl;
}
D题
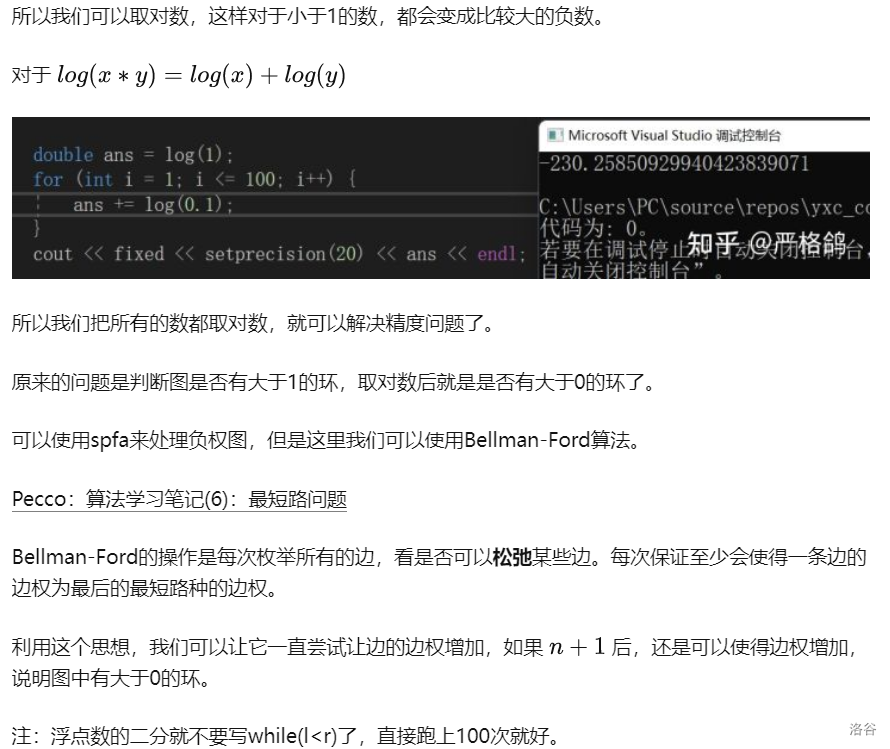
Link with Game Glitch

#include<bits/stdc++.h>
using namespace std;
double a[2005],c[2005],w[2005];
int b[2005],d[2005],u[2005],v[2005];
int n,m;
double dist[1005];
int check(double x)
{
for(int i = 1;i<=m;++i)
u[i] = b[i],v[i] = d[i],w[i] = -log(c[i]*x/a[i]);
for(int i = 1;i<n;++i)
for(int j = 1;j<=m;++j)
if(dist[u[j]]+w[j]<dist[v[j]])
dist[v[j]] = dist[u[j]]+w[j];
for(int i = 1;i<=m;++i)
if(dist[u[i]]+w[i]<dist[v[i]])
return 0;
return 1;
}
int main()
{
cin>>n>>m;
for(int i = 1;i<=m;++i)
cin>>a[i]>>b[i]>>c[i]>>d[i];
double l = 0,r = 1;
while(r-l>=1e-8)
{
double mid = (l+r)/2;
if(check(mid)) l = mid;
else r = mid;
}
printf("%.8lf",l);
return 0;
}
L题
Link with Level Editor I

因为每个相邻世界之间最多选一条边 所以不用建图 直接转移就好
f[i][j] 表示到达第i个世界第j个点 经过世界的最小值
初始状态:0x3f f[i][1]=0
终止状态:min{f[i][m]}
转移:(1)i-1世界 j点 直接到 i世界 j点 f[i][j]=min(f[i][j],f[i-1][j]+1)
(2)i-1世界u点 到 i世界 j点 f[i][j]=min(f[i][j],f[i-1][u]+1)
因为空间有限 所以用到滚动数组
#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define ll long long
const int maxn=2e3+5;
int f[maxn],g[maxn];
int n,m,ans=1e9+7;
int main(){
cin>>n>>m;
memset(g,0x7f,sizeof(g));
g[1]=0;
for(int i=1;i<=n;i++){
int num,u,v;
memset(f,0x7f,sizeof(f));
f[1]=0;
scanf("%d",&num);
for(int j=1;j<=num;j++){
scanf("%d%d",&u,&v);
f[v]=min(g[u]+1,f[v]);
}
for(int j=1;j<=m;j++)
f[j]=min(f[j],g[j]+1);
for(int j=1;j<=m;j++)
g[j]=f[j];
ans=min(f[m],ans);
}
if(ans>n)cout<<"-1"<<endl;
else cout<<ans<<endl;
return 0;
}
H题:
Take the Elevator
题意:
n个人坐电梯,楼高 k ,每个人有起始楼层和目标楼层。
电梯有载客量限制 m ,上升时可以上升到任意层并随时下降,但是下降 要一直下降到一层才能再上升。
电梯每秒运行一层,换方向和上下人不占用时间,问电梯最短运行时间

//By cls1277
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
#define Fo(i,a,b) for(LL i=(a); i<=(b); i++)
#define Ro(i,b,a) for(LL i=(b); i>=(a); i--)
#define Eo(i,x,_) for(LL i=head[x]; i; i=_[i].next)
#define Ms(a,b) memset((a),(b),sizeof(a))
#define endl '\n'
const LL maxn = 2e5+5;
LL n, m, k, w, c1, c2;
LL ans1[maxn], ans2[maxn];
struct Node {
LL ops, weight;
};
vector<Node> a, b;
bool operator < (const Node &x, const Node &y) {
if(x.ops!=y.ops) return x.ops>y.ops;
return x.weight<y.weight;
}
int main() {
cin>>n>>m>>k;
Fo(i,1,n) {
LL x, y; cin>>x>>y;
if(x<y) {
a.push_back({x, -1});
a.push_back({y, 1});
} else {
b.push_back({x, 1});
b.push_back({y, -1});
}
}
sort(a.begin(), a.end());
sort(b.begin(), b.end());
for(auto it:a) {
w += it.weight;
if(w > m*c1) ans1[++c1] = it.ops;
}
w = 0;
for(auto it:b) {
w += it.weight;
if(w > m*c2) ans2[++c2] = it.ops;
}
LL c = max(c1, c2), ans = 0;
Fo(i,1,c) {
ans += (max(ans1[i], ans2[i])-1)*2;
}
cout<<ans;
return 0;
}
I 题
let fat tension

其实就是很简单的线性代数 满足结合律
保证了每次矩阵乘法三重循环中只有一个n (因为n方的复杂度是会超的)
#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define ll long long
const int maxn=1e4+5;
double X[maxn][55],Y[maxn][55],T[55][maxn],TT[55][55],ans[maxn][55];
int n,k,d;
int main(){
cin>>n>>k>>d;
for(int i=1;i<=n;i++){
double all=0;
for(int j=1;j<=k;j++){
scanf("%lf",&X[i][j]);
all+=X[i][j]*X[i][j];
}
all=sqrt(all);
for(int j=1;j<=k;j++)
X[i][j]/=all,T[j][i]=X[i][j];
}
for(int i=1;i<=n;i++)
for(int j=1;j<=d;j++)
scanf("%lf",&Y[i][j]);
for(int i=1;i<=k;i++)
for(int j=1;j<=d;j++)
for(int z=1;z<=n;z++)
TT[i][j]+=T[i][z]*Y[z][j];
for(int i=1;i<=n;i++)
for(int j=1;j<=d;j++)
for(int z=1;z<=k;z++)
ans[i][j]+=X[i][z]*TT[z][j];
for(int i=1;i<=n;i++){
for(int j=1;j<=d;j++)
printf("%.8lf ",ans[i][j]);
printf("\n");
}
return 0;
}



