**浅谈差分【复习】**
https://www.luogu.org/problem/P5026
分析:
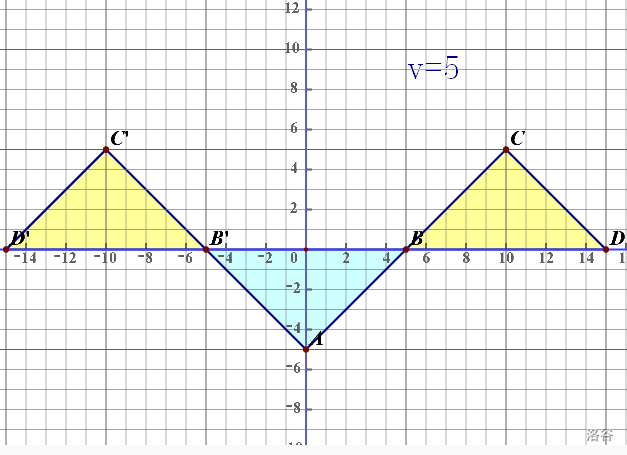
区间加上一个等差序列,两次差分完成
code :
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
int n,m;
int aa[2100000],bb[2100000];
#define isdigit(x) ((x)>='0'&&(x)<='9')
inline int read(){
int a=0,flag=1;
char c=getchar();
while(!isdigit(c)){
if(c=='-')flag=-1;
c=getchar();
}
while(isdigit(c)){
a=(a<<1)+(a<<3)+c-48;
c=getchar();
}
return a*flag;
}
int main(){
n=read(),m=read();
int *a=aa+1000000,*b=bb+1000000;
for(int i=1;i<=n;++i){
int v=read(),x=read();
a[x-3*v+1]++;
a[x-2*v+1]-=2;
a[x+1]+=2;
a[x+2*v+1]-=2;
a[x+3*v+1]++;
}
for(int i=-40000;i<=m+40000;++i)a[i]+=a[i-1],b[i]+=b[i-1]+a[i];
for(int i=1;i<=m;++i)printf("%d ",b[i]);
return 0;
}
https://www.luogu.org/problem/P4623
分析:
对x轴和y轴分别维护一个树状数组,
支持区间加和单点查询,用差分
code by wzxbeliever:
#include<bits/stdc++.h>
#define ll long long
#define il inline
#define ri register int
#define lowbit(x) x&(-x)
using namespace std;
const int maxn=1e5+5;
const int maxx=1e6+5;
int n,m,a,b,c,d,e,f,val;
int X[maxx],Y[maxx];
char ch1,ch2;
il void add(int x,int p){while(x<=maxx)X[x]+=p,x+=lowbit(x);}
il int query(int x){int res=0;while(x)res+=X[x],x-=lowbit(x);return res;}
il void add2(int x,int p){while(x<=maxx)Y[x]+=p,x+=lowbit(x);}
il int query2(int x){int res=0;while(x)res+=Y[x],x-=lowbit(x);return res;}
int main(){
scanf("%d",&n);
for(ri i=1;i<=n;i++){
int Lmin,Rmin,Lmax,Rmax;
Lmax=Rmax=0;Lmin=Rmin=maxx;
scanf("%d%d%d%d%d%d",&a,&b,&c,&d,&e,&f);
a++,b++,c++,d++,e++,f++;
Lmin=min(a,min(c,e));
Rmin=min(b,min(d,f));
Lmax=max(a,max(c,e));
Rmax=max(b,max(d,f));
Lmin++;Rmin++;
add(Lmin,1);add(Lmax,-1);
add2(Rmin,1);add2(Rmax,-1);
}
scanf("%d",&m);
while(m--){
cin>>ch1>>ch2>>val;val++;
if(ch1=='x')printf("%d\n",query(val));
else printf("%d\n",query2(val));
}
return 0;
}
https://www.luogu.org/problem/P2680
分析:
很早就做过了,现在发现又不会了
模仿一下考试过程:
一棵树,m个计划,可将一条边权附为0 ,最大值最小
典型的二分答案:
关键在于check()函数怎么写
考虑此时小于mid的路径都不会产生影响了
大于mid的所有边中,如果存在一条公共边,它的边权为k
使得减掉k之后所有边都小于等于mid
则return true 否则 return false
剩下就是统计出这条公共边了
用树上差分统计
总的来说就是
LCA+树上差分+二分
code by std:
#include<bits/stdc++.h>
#define IL inline
#define RI register int
#define N 300008
using namespace std;
IL void in(int &x)
{
int f=1;x=0;char s=getchar();
while(s>'9' or s<'0'){if(s=='-')f=-1;s=getchar();}
while(s>='0' and s<='9'){x=x*10+s-'0';s=getchar();}
x*=f;
}
struct node{
int x , y , lca , dis ;
bool operator < (const node & a ) const {
return dis < a.dis ;
}
}query[N];
int depth[N],f[N][21],Dis[N],n,head[N],tot,k,ans,init[N],cnt[N];
struct cod{int u,v,w;}edge[N<<1];
int l,r,m;
IL void add(int x,int y,int z)
{
edge[++tot].u=head[x];
edge[tot].v=y;
edge[tot].w=z;
head[x]=tot;
}
void dfs(int u,int fa , int dis)
{
depth[u]=depth[fa]+1;
f[u][0]=fa ; init[u] = dis;
for(RI i=1;(1<<i)<=depth[u];i++)
f[u][i]=f[f[u][i-1]][i-1];
for(RI i=head[u];i;i=edge[i].u)
{
if(edge[i].v==fa)continue;
Dis[edge[i].v]=Dis[u]+edge[i].w;
dfs(edge[i].v,u,edge[i].w);
}
}
IL int lca(int x,int y)
{
if(depth[x]>depth[y])swap(x,y);
for(RI i=20;i>=0;i--)
if(depth[y]-(1<<i)>=depth[x])
y=f[y][i];
if(x==y)return x;
for(RI i=20;i>=0;i--)
{
if(f[x][i]==f[y][i])continue;
x=f[x][i],y=f[y][i];
}
return f[x][0];
}
void dfss(int u,int fa)
{
for(RI i=head[u];i;i=edge[i].u)
{
if(edge[i].v==fa)continue;
dfss(edge[i].v,u);
cnt[u]+=cnt[edge[i].v];
}
}
IL bool ok(int x)
{
int num=0,now=0;
for(RI i=1;i<=n;i++)cnt[i]=0;
for(RI i=1;i<=m;i++)
{
if(query[i].dis<=x)continue;
cnt[query[i].x]++;cnt[query[i].y]++;
cnt[query[i].lca]-=2;
num++;
}
dfss(1,0);
for(RI i=1;i<=n;i++)
{
if(cnt[i]==num)now=max(now,init[i]);
}
return query[m].dis-now<=x;
}
int main()
{
in(n),in(m);
for(RI i=1,x,y,z;i<n;i++)
{
in(x),in(y),in(z);
add(x,y,z);add(y,x,z);
}
dfs(1,0,0);
for(RI i=1,x,y;i<=m;i++)
{
in(x),in(y);
query[i].lca=lca(x,y);
r=max(r,(query[i].dis=Dis[x]+Dis[y]-2*Dis[query[i].lca]));
query[i].x = x,query[i].y = y;
}
sort(query+1,query+m+1);
while(l<=r)
{
int mid=(l+r)>>1;
if(ok(mid))r=mid-1;
else l=mid+1;
}
printf("%d",l);
}
盗取衡水的一道题:居然和jklover以前出的题一样
题目描述
科学家在“无限神机”(Infinity MachineInfinity Machine)找到一个奇怪的机制,这个机制有NN个元件,有MM条电线连接这些元件,所有元件都是连通的。两个元件之间可能有多条电线连接。
科学家对这些元件可以任意地设置为“高电压”和“低电压”两种模式,如果一条电线的一端为高电压,另一端为低电压,这条电线就会产生电流。
为了安全的研究“无限神机”,科学家需要找到一条电线,将它的两端设为相同的电压,并且除选择的这条电线外,其它所有电线都有电流(否则就没有研究的价值了)。
有多少条电线满足这样的条件?
分析:
像这种只有两个对立面的,一般和二分图,奇环,偶环有关
首先偶环上的边肯定没法删,也可以说是不用删
再考虑奇环,首先一个奇环一定是要删一条边的,
但是如果有多个奇环,但是你又只能删一条边怎么办?
那这条边就必须被所有奇环都覆盖,并且不能再偶环上
边覆盖问题差分维护 边差分
还要注意的是这里差分没有用到LCA
因为此时lca(a,b)==a||b
还有就是这个代码里的in数组很是巧妙
code:
#include<bits/stdc++.h>
using namespace std;
struct rec{int nxt,to;bool dead;}e[400002];
int head[100001],cnt=1;
int n,m;
int odd[100001],eve[100001],cut[400002],depth[100001],in[100001];
bool vis[100001];
int ans;
void add(int x,int y)
{
e[++cnt].nxt=head[x];
e[cnt].to=y;
head[x]=cnt;
}
void dfs(int x)
{
vis[x]=1;
for(int i=head[x];i;i=e[i].nxt)
{
if(cut[i])continue;
cut[i]=cut[i^1]=1;
if(vis[e[i].to])
{
if((depth[x]-depth[e[i].to])&1){eve[e[i].to]--;eve[x]++;}
else{odd[e[i].to]--;odd[x]++;odd[0]++;}
}
else
{
depth[e[i].to]=depth[x]+1;
in[e[i].to]=i;
dfs(e[i].to);
}
}
}
void dfs(int x,int f)
{
for(int i=head[x];i;i=e[i].nxt)
if(in[e[i].to]==i)
{
dfs(e[i].to,x);
odd[x]+=odd[e[i].to];
eve[x]+=eve[e[i].to];
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
int u,v;
scanf("%d%d",&u,&v);
add(u,v);add(v,u);
}
for(int i=1;i<=n;i++)if(!vis[i])dfs(i);
if(odd[0]==1)ans=1;
for(int i=1;i<=n;i++)if(!in[i])dfs(i,0);
for(int i=1;i<=n;i++)
if(in[i]&&odd[i]==odd[0]&&!eve[i])ans++;
printf("%d",ans);
return 0;
}

分析:
考虑维护差分数组
对于区间加[L,R],发现区间里的数的贡献不会变动,只有L-1,L+1,R+1,R
这四个位置的数的贡献可能会变
所以特判一下,利用树状数组维护前缀和
code by std:
#include <cstdio>
#define maxn 200005
#define lowbit(x) (x&(-(x)))
#define LL long long
LL a[maxn];
int n,m;
struct TreeArr{
int a[maxn];
void add(int x,int v){
while(x<=n){
a[x]+=v;
x+=lowbit(x);
}
}
int query(int pos){
int ret=0;
while(pos){
ret+=a[pos];
pos^=lowbit(pos);
}
return ret;
}
} tree;
bool check(int x){
return (a[x]<0&&a[x+1]>0)||(a[x]>0&&a[x+1]<0);
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%lld",&a[i]);
for(int i=n;i>=1;i--){
a[i]-=a[i-1];
if(a[i]*a[i+1]<0)tree.add(i,1);
}
for(int i=1;i<=m;i++){
int op;scanf("%d",&op);
if(op){
int x,y,z;scanf("%d%d%d",&x,&y,&z);
int px=check(x),py=check(y);
int px1=check(x-1),py1=check(y+1);
a[x]+=z;a[y+1]-=z;
int nx=check(x),ny=check(y);
int nx1=check(x-1),ny1=check(y+1);
tree.add(x,nx-px);
if(x>1)tree.add(x-1,nx1-px1);
if(x!=y)tree.add(y,ny-py);
tree.add(y+1,ny1-py1);
}
else {
int x,y;scanf("%d%d",&x,&y);
if(x==y)printf("0\n");
else printf("%d\n",tree.query(y-1)-tree.query(x));
}
}
}



