杂题训练之十一

meet in the middle

https://www.luogu.org/problem/P4799

下面引出主角——折半搜索（meet in the middle思想）

因为N≤40 O(2⁴⁰)的爆搜一定会TLE，所以我们将N分成两份

搜索11到n/2和n/2+1到n，让复杂度降到O(2^n/2+1+组合答案的复杂度))。

画一个图（网上找的不错的图）理解一下为什么能降低复杂度

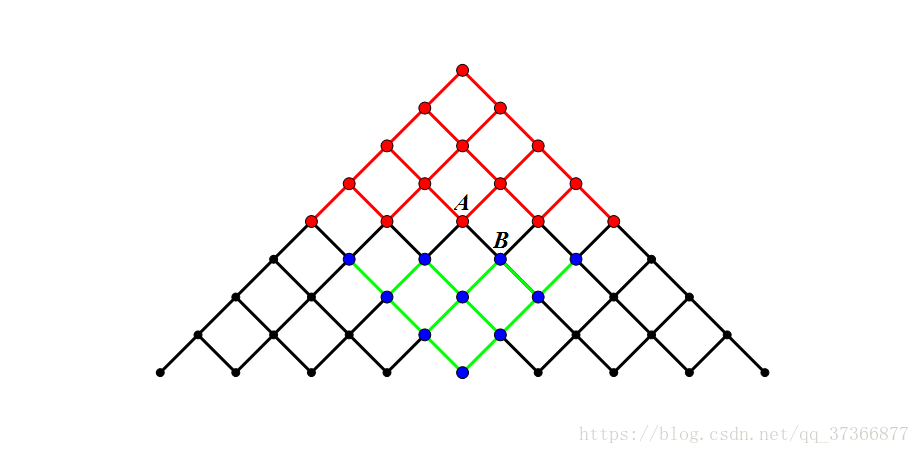
分析：

双向搜索往往也用来解决这种N等于三四十的搜索问题

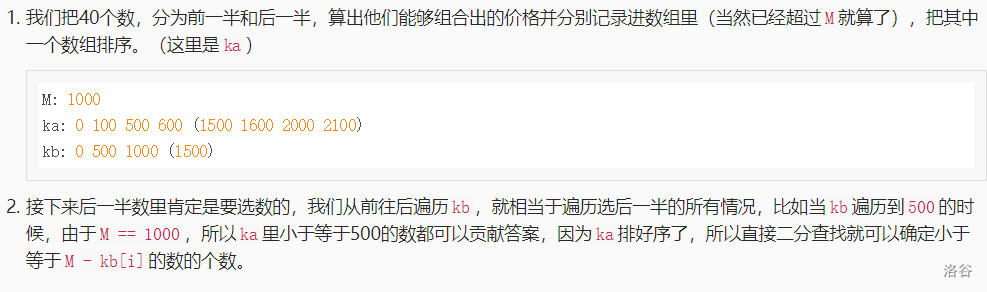
code by std：

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cctype>
#define ll long long
#define R register
#define N 55
using namespace std;
template<typename T>inline void read(T &a){
    char c=getchar();T x=0,f=1;
    while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
    while(isdigit(c)){x=(x<<1)+(x<<3)+c-'0';c=getchar();}
    a=f*x;
}
ll n,m,w[N],mid,suma[1<<21],sumb[1<<21],cnta,cntb,ans;
inline void dfs(R int l,R int r,R ll sum,R ll a[],R ll &cnt){
    if(sum>m)return;
    if(l>r){
        a[++cnt]=sum;
        return;
    }
    dfs(l+1,r,sum+w[l],a,cnt);
    dfs(l+1,r,sum,a,cnt);
}
int main(){
    read(n);read(m);
    for(R int i=1;i<=n;i++)read(w[i]);
    mid=n>>1;
    dfs(1,mid,0,suma,cnta);
    dfs(mid+1,n,0,sumb,cntb);
    sort(suma+1,suma+1+cnta);
    for(R int i=1;i<=cntb;i++)
        ans+=upper_bound(suma+1,suma+1+cnta,m-sumb[i])-suma-1;
    printf("%lld\n",ans);
    return 0;
}