动态规划训练之十七
https://projecteuler.net/problem=638
题目描述:
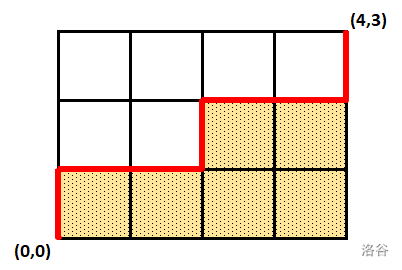
求所有(0,0)走到(n,m)路线(k^矩形个数)
分析:
考虑如果只是求方案数的话
很简单一个递推dp[i,j]=dp[i-1,j]+dp[i,j-1];
也是一个组合数C(n+m,n)
再考虑把面积加上进行递推
性质ki+j==ki*kj
重新定义dp[i,j]:走到(i,j)之前所有方案的k矩形个数和
如果我们考虑每次竖着看一列矩形的面积时:
dp[i,j]=dp[i,j-1]×kj+dp[i-1,j]
如果我们考虑每次横着看一排矩形的面积时:
dp[i,j]=dp[i,j-1]+dp[i-1,j]×ki
考虑将两个式子进行合并
dp[i,j-1]×(kj-1)=dp[i-1,j]×(ki-1)
令j=j-1(转化为dp[i,j]这样的形式)
dp[i,j]×(kj+1-1)=dp[i-1,j+1]×(ki-1)
同理dp[i-1,j+1]×(kj+2-1)=dp[i-2,j+2]×(ki-1-1)
最后一定会到达终止边界dp[0,i+j]=1
所以dp[i,j]=(ki-1)×(ki-1-1)×....(k1-1)/(kj-1)×(kj+1-1)×.....×(kj+i-1-1)
这样直接线性递推就好
因为只用交答案,慢点也无所谓



