概率期望训练之二

https://www.luogu.org/problem/P4550

这里有个很好的结论：

概率正向推，期望反向推

对于这个题而言，是要求期望花费

而这个期望花费又与期望次数有关

所以先算出期望次数，再去推期望花费

设f[i]表示购买了i种物品，还要购买物品的期望次数（反向推）

可以得出

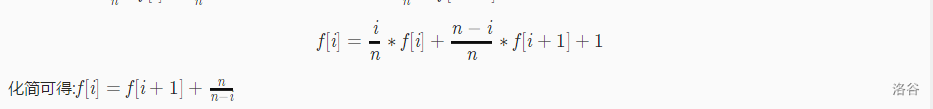
再设g[i]表示购买了i种物品，还要购买物品的期望花费（反向推）

可以得出

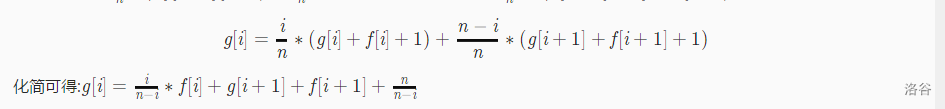
这里你再来想一想为什么要反向推，因为f[n]=0,g[n]=0,而如果正向推得话f[1]=?又g[1]=?

code：

#include <bits/stdc++.h>
using namespace std;
int n;
double f[10005],g[10005];
int main() {
    scanf("%d",&n);
    for(int i=n-1;~i;--i) {
        f[i]=f[i+1]+(1.0*n)/(1.0*(n-i));
        g[i]=(1.0*i)/(1.0*(n-i))*(f[i]+1)+g[i+1]+f[i+1]+1;
    }
    printf("%.2lf\n",g[0]);
    return 0;
}