浅谈prufer编码

树的prufer编码

prufer是无根树的一种编码方式，一棵无根树和一个prufer编码唯一对应，也就是一棵树有唯一的prufer编码，而一个prufer编码对应一棵唯一的树。

注意这个唯一性！！！！

第一部分：树编码成prufer序列。

树编码成prufer序列的方式是：prufer序列初始为空。每次从树上选出一个编号最小的叶子节点，然后将与该叶子节点相邻的那个节点的编号写入prufer序列的末尾，之后从树上删掉这个叶子节点。循环这个步骤n-2次，最后得到一个长度为n-2的prufer序列（此时树中只有一条边，我们就不管它了）。

我们以下面这个树为例。

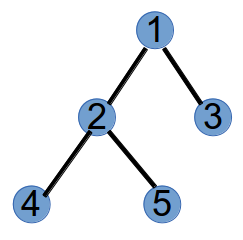
step1:编号最小的叶子节点为3，将与其相连的节点1加到prufer的末尾，并将3从树上删掉，此时prufer序列为(1)，树变为如下：

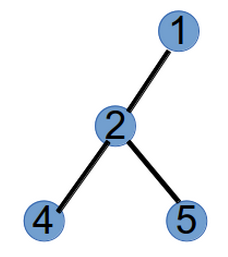
step2:编号最小的叶子节点为1，将与其相连的节点2加到prufer末尾，此时prufer序列为(1,2),并将节点1删掉，树变为如下：

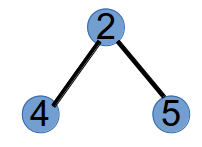
step3:编号最小的叶子节点为4，将与其相连的节点2加入到prufer的末尾，此时prufer序列为(1,2,2)，并将节点4删掉，树变为如下：

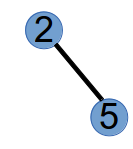
此时，结束，我们得到了prufer序列为(1,2,2)。

第二部分：由prufer序列得到树。首先，将每个节点的度数设为1加上该节点在prufer序列中出现的次数。然后以下循环执行n-2次。第i次循环，选择此时度数为1的编号最小的节点u，将其与此时prufer序列的第i个元素v连边，然后将u和v的度数都减去1。这n-2次执行完之后，仅剩下两个节点他们的度数都是1，将这两个点连边，这样就得到一个有n-1条边的树。

下面，我们以上面的prufer序列为例还原这个树。初始的prufer为(1,2,2)，初始的度数为：

step1：选择度数为1的最小编号的节点3与prufer的第一个元素1连边，并将3和1的度数都减去1，得到树和新的度数：

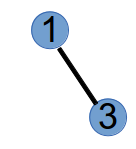
step2：选择度数为1的最小节点1和prufer中的第二个元素2连边，并将1和2的度数都减去1，得到树和新的度数：

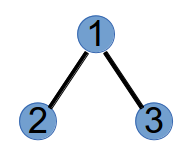
step3：选择度数为1的最小节点4和prufer中的第三个元素2连边，并将4和2的度数都减去1，得到树和新的度数：

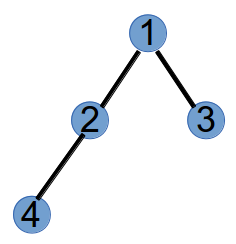
最后，将仅有的度数为1的两个节点2和5，连边，得到：

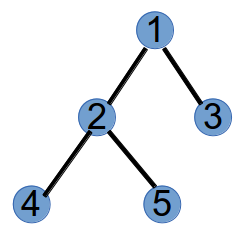
假设告诉我们每个点的度数，则这颗树的种类数就有下式

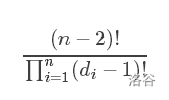
没错可重复元素的排列

prufer序列的性质及相关结论

• 重要性质：prufer序列与无根树一一对应。
• 度数为di的节点会在prufer序列中出现di-1次。
• 一个n个节点的完全图的生成树个数为n^(n-2)。(n的n-2次方)
• 还有就是那个可重复元素的排列公式

例题一

https://www.luogu.org/problem/P2624

本题唯一不同的点就是有的结点度数没有限制（就是没法确定，只要满足能行，是多少都可以）

高精不会写，代码是抄的，再说了复赛应该不会考高精度的，如果考了的话那我就是该背时

code：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <cctype>

using namespace std;

int read()
{
    int x=0,f=1;char ch=getchar();
    while (!isdigit(ch)){if (ch=='-') f=-1;ch=getchar();}
    while (isdigit(ch)){x=x*10+ch-48;ch=getchar();}
    return x*f;
}

int n,cnt,d[1050],sum,tot;

struct BigInt
{
    int num[10000],len;

    BigInt()
    {
        memset(num,0,sizeof(num));
        len=1;
    }

    BigInt operator* (const int &rhs) const
    {
        BigInt ans;
        ans.len=len+6;
        for (int i=1;i<=len;i++)
            ans.num[i]+=num[i]*rhs;
        for (int i=1;i<ans.len;i++)
            if (ans.num[i]>9)
            {
                ans.num[i+1]+=ans.num[i]/10;
                ans.num[i]%=10;
            }
        while (!ans.num[--ans.len])
        return ans;
    }

    BigInt operator/ (const int &rhs) const
    {
        BigInt ans=*this;
        ans.len++;
        for (int i=ans.len;i;i--)
        {
            ans.num[i-1]+=ans.num[i]%rhs*10;
            ans.num[i]/=rhs;
        }
        while (!ans.num[--ans.len]);
        return ans;
    }
}ans;

int main()
{
    n=read();
    for (int i=1;i<=n;i++)
    {
        d[i]=read();
        if (!d[i])
        {
            puts("0");
            return 0;
        }
        if (d[i]!=-1)
        {
            sum+=d[i]-1;
            cnt++;
        }
    }
    if (sum>2*n-2)
    {
        puts("0");
        return 0;
    }
    ans.num[1]=1;
    for (int i=n-1-sum;i<n-1;i++)
        ans=ans*i;
    for (int i=1;i<=n-2-sum;i++)
        ans=ans*(n-cnt);
    for (int i=1;i<=n;i++)
    {
        //cout << i << " " << ans.len << endl;
        for (int j=2;j<=d[i]-1;j++)
            ans=ans/j;
    }
    //cout << ans.len << endl;
    //system("pause");
    for (int i=ans.len;i;i--)
        printf("%d",ans.num[i]);
    return 0;
}