博弈论训练之一

阶梯NIm

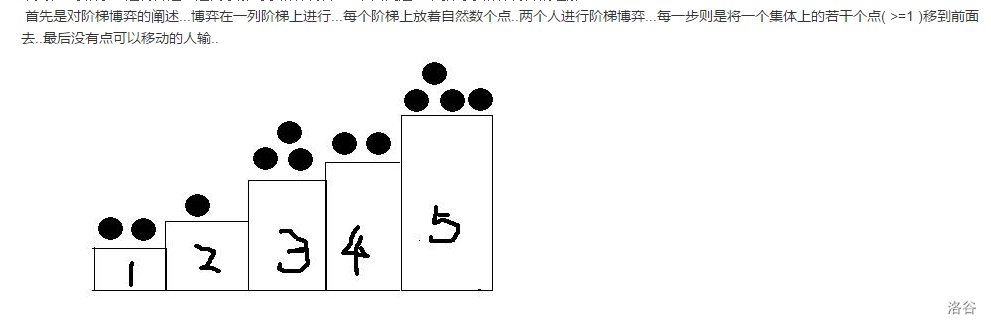
如这就是一个阶梯博弈的初始状态 2 1 3 2 4 ... 只能把后面的点往前面放...如何来分析这个问题呢..

其实阶梯博弈经过转换可以变为Nim..

把所有奇数阶梯看成N堆石子..做nim

把石子从奇数堆移动到偶数堆可以理解为拿走石子..就相当于几个奇数堆的石子在做Nim

证明（可能写（chao）的很多，但真的很好理解）

假设我们是先手...所给的阶梯石子状态的奇数堆做Nim先手能必胜...我就按照能赢的步骤将奇数堆的石子移动到偶数堆...如果对手也是移动奇数堆..我们继续移动奇数堆..如果对手将偶数堆的石子移动到了奇数堆..那么我们紧接着将对手所移动的这么多石子从那个奇数堆移动到下面的偶数堆...两次操作后...相当于偶数堆的石子向下移动了几个..而奇数堆依然是原来的样子...即为必胜的状态...就算后手一直在移动偶数堆的石子到奇数堆..我们就一直跟着他将石子继续往下移..保持奇数堆不变...如此做下去..我可以跟着后手把偶数堆的石子移动到0..然后你就不能移动这些石子了...所以整个过程..将偶数堆移动到奇数堆不会影响奇数堆做Nim博弈的过程..整个过程可以抽象为奇数堆的Nim博弈...
其他的情况...先手必输的...类似推理...只要判断奇数堆做Nim博弈的情况即可...
为什么是只对奇数堆做Nim就可以...而不是偶数堆呢？

因为起手是1（奇数）

https://www.luogu.org/problem/P2575

首先我们知道一个状态为必败态，当且仅当它能到达的所有状态都是必胜态。一个状态为必胜态，当且仅当它能到达的所有状态中有一个必败态

问题转化为阶梯博弈

code：

#include<iostream>
#include<cstdio>
#include<cstring>
#define N 27
using namespace std;
int T,n;
bool vis[N];
int main()
{
    scanf("%d",&T);
    while(T--)
    {
        int ans=0;
        scanf("%d",&n);
        for(int i=1;i<=n;++i)
        {
            int now=0,num;
            memset(vis,0,sizeof(vis));
            scanf("%d",&num);
            for(int j=1;j<=num;++j)
            {
                int in;
                scanf("%d",&in);
                vis[in]=1;
            }
            int cnt=0,tot=0;
            for(int j=20;j>=0;--j)
            {
                if(!vis[j])
                {
                    if(tot)
                    {
                        ans^=tot;
                        tot=0;
                    }
                    cnt^=1;
                }
                else
                    if(cnt)
                        ++tot;
            }
            if(tot)
                ans^=tot;
        }
        printf("%s\n",ans?"YES":"NO");
    }
    return 0;
}