杂题训练之七

https://www.luogu.org/problem/P1663

首先这题的数据范围比较水，O(N*N)可以过，但就不说了

考虑小一点

问题转化为要找到所有直线相交的最高点

考虑二分答案，

大于这个答案的一定可以过，但不一定最小

小于这个答案的无法满足条件

所以可以二分答案

再就考虑check函数怎么判断

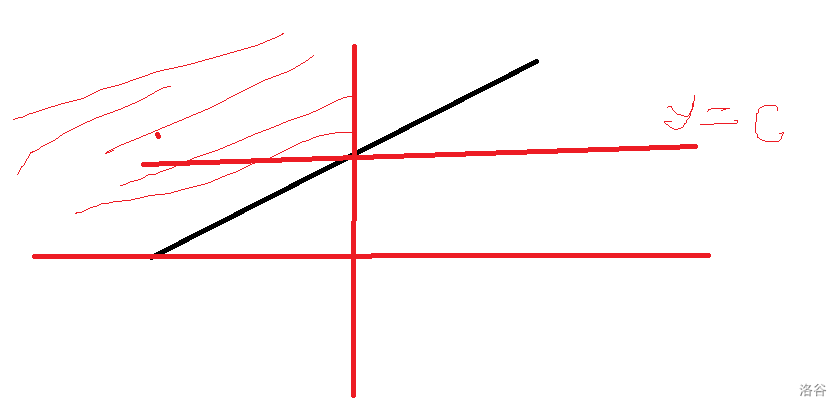
考虑此时二分的答案为C，交于斜率>0的直线于一点，该点左边部分一定可以取到

同理斜率<0的直线

讲得可能不大清楚，但是代码很清晰的

code：

#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn=5005;
struct ad{ int x,y; } a[maxn];
struct line{ double k,b; } b[maxn];   //存直线的表达式
int n; double l,r,mid,L,R,ans;
inline int read(){
    int ret=0; char ch=getchar();
    while (ch<'0'||ch>'9') ch=getchar();
    while (ch>='0'&&ch<='9') ret=ret*10+ch-'0',ch=getchar();
    return ret;
}
inline bool check(double x){
    L=-2e9,R=2e9;
    for (int i=1;i<n;i++){
        if (b[i].k<0) L=max(L,(x-b[i].b)/b[i].k);    //由于k可能小于0，注意不等式两边同除以负数要变号
        if (b[i].k>0) R=min(R,(x-b[i].b)/b[i].k);
        if (b[i].k==0&&b[i].b>x) return 0;    //k等于0的话一除就暴了，注意特判
    }
    return L<=R;
}
int main(){
    freopen("hill.in","r",stdin);
    freopen("hill.out","w",stdout);
    n=read();
    for (int i=1;i<=n;i++) a[i].x=read(),a[i].y=read();
    for (int i=1;i<n;i++){
        b[i].k=1.0*(a[i].y-a[i+1].y)/(a[i].x-a[i+1].x);      //自己推一下的话，应该能懂
        b[i].b=1.0*a[i].y-b[i].k*a[i].x;
    }
    l=0,r=1000000;
    while (r-l>=0.001){    //二分小数的办法
        mid=(l+r)/2.0;
        if (check(mid)) ans=r=mid; else l=mid;
    }
    printf("%.2lf\n",ans);
    return 0;
}