浅谈博弈论

引言

在生活中五子棋也是一种先手有必赢策略的游戏，有人会说五子棋先手我也会输啊，所以

博弈论问题都有个类似如“参与者足够聪明”，“两人都不犯错"的前提。

在此前提下，讨论几种常见的博弈情形

一：巴什博弈

问题描述：n个物品，两个人轮流取[1,m]个，最后取光者胜利，判断先手胜还是后手胜？

? 分析

考虑到若n=m+1 那么 第一个人不论如何取都不能取胜。

? 进一步我们发现若 n=k*(m+1)+r; 先取者拿走 r 个，那么后者再拿[1,m]个

? n=（k-1）*（m+1）+s；先取者再拿走s 个最后总能造成剩下n=m+1 的局面。

? 因此，此时先手有必赢策略。

? 相对应的，若n=k*(m+1) 那么先取者必输。

二：尼姆博弈(Nimm Game)

问题描述：n堆物品，第i堆有ai个，两个人轮流选择一堆，并从中选取走[1,ai]个，最后取光者胜利，判断先手胜利还是后手胜利？

分析：

先说点别的：

N必胜状态，P必败状态

N一定是从P转移过来的，P一定不能从N转移过来（但可能p的后继状态里有N，只是不会转移过去）

为什么呢？

比如说，你现在处于优势，你不可能把你再陷入劣势

你现在处于劣势，你肯定要想尽方法把你带进优势

Nim游戏有个定理

先手必胜，当且仅当a1xora2xora3xor.....xoran!=0

为什么呢？为了方便把前面这一坨xor设为Y

如果Y=0，则一定不存在一个k，使得Yxork==0

如果Y!=0，则一定存在一个K，使得Yxork==0

同理N和P，证毕

三.SG函数

先定义一个

Mex运算：****最小不属于这个集合的最小整数

例如mex{0,1,2,4}=3、mex{2,3,5}=0、mex{}=0

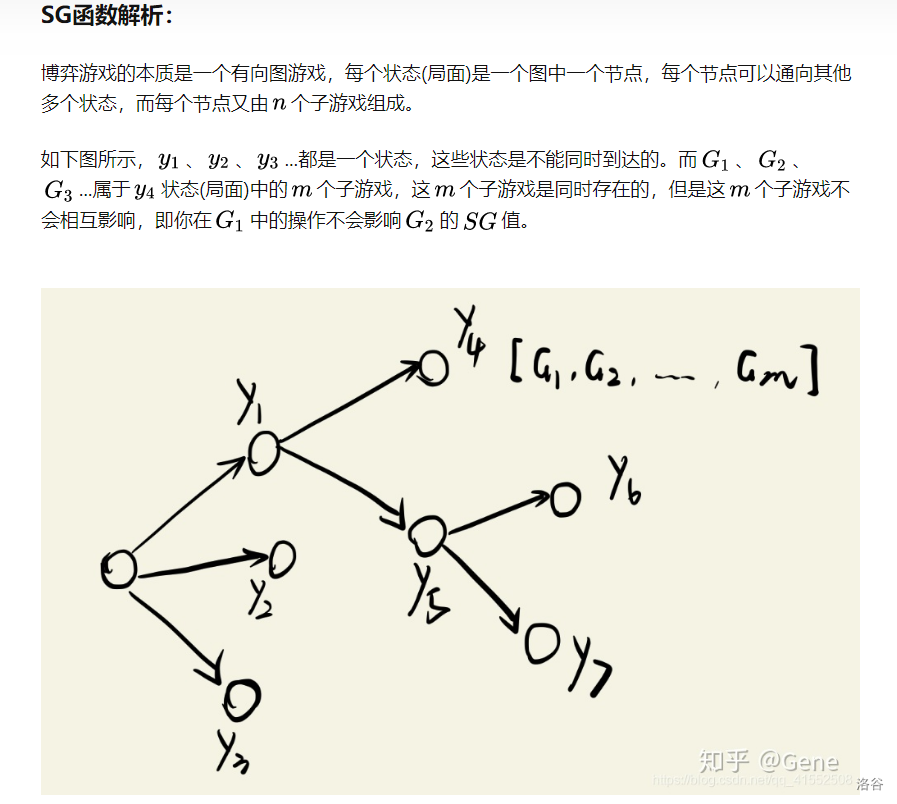
对于一个给定的有向无环图，定义关于图的每个顶点的SG函数g如下：

g(x)=mex{ g(y) | y是x的后继（y可能会有多个）}。（这个公式很重要，反复看）

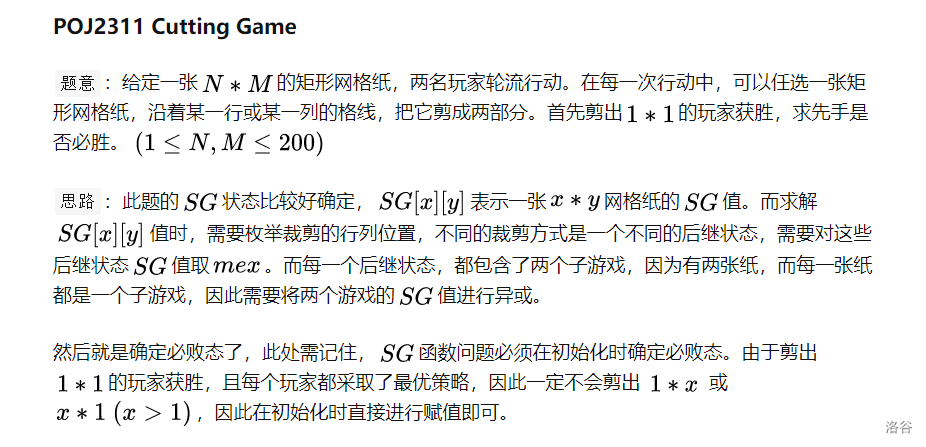
首先定义SG[x]表示当前堆石子个数为x时的SG值明显的有SG[0]=0

我们要依次处理出每一个数的SG值我们知道当前状态的SG值为所有后继状态的SG值取mex

所有我们从小到大进行处理就好

做完这个题发现其实尼姆博弈就是就是SG[x]=x的特殊情况罢了

#include <cstdio>
#include <cstring>
const int maxn=1005;
int f[maxn],SG[maxn],vis[maxn];
 
void getSG(int n){
    for(int i=1;i<=n;i++){
        memset(vis,0,sizeof(vis));
        for(int j=1;f[j]<=i;j++) vis[SG[i-f[j]]]=1;
        for(int j=0;j<=n;j++){
            if(!vis[j]){
                SG[i]=j;
                break;
            }
        }
    }
}
 
int main(){
    f[0]=f[1]=1;
    for(int i=2;i<=16;i++) f[i]=f[i-1]+f[i-2];
    getSG(1000);
    int m,n,p;
    while(scanf("%d%d%d",&m,&n,&p)==3){
        if(m==0&&n==0&&p==0) break;
        if(SG[m]^SG[n]^SG[p]) puts("Fibo");
        else puts("Nacci");
    }
    return 0;
}

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#define __ ios::sync_with_stdio(0);cin.tie(0);cout.tie(0)
#define rep(i,a,b) for(int i = a; i <= b; i++)
#define LOG1(x1,x2) cout << x1 << ": " << x2 << endl;
#define LOG2(x1,x2,y1,y2) cout << x1 << ": " << x2 << " , " << y1 << ": " << y2 << endl;
#define LOG3(x1,x2,y1,y2,z1,z2) cout << x1 << ": " << x2 << " , " << y1 << ": " << y2 << " , " << z1 << ": " << z2 << endl;
typedef long long ll;
typedef double db;
const int N = 1000+10;
const int M = 1e5+100;
const db EPS = 1e-9;
using namespace std;

int sg[N],n;

int solve(int x)
{
    if(sg[x] != -1) return sg[x];
    int vis[2010]; memset(vis,0,sizeof vis);
    int ans[2010]; //记录每一个约数
    int tp = 0, ct = 0;
    rep(i,1,x-1){
        if(x%i == 0){
            ans[++ct] = solve(i);
            tp ^= ans[ct];
        }
    }
    rep(i,1,ct) vis[tp^ans[i]] = 1; //枚举每一个子状态
    rep(i,0,2000)
        if(vis[i] == 0) return sg[x] = i;
}

int main()
{
    memset(sg,-1,sizeof sg);
    sg[1] = 0;
    while(~scanf("%d",&n)){
        int ans = 0;
        rep(i,1,n){
            int xx; scanf("%d",&xx);
            ans ^= solve(xx);
        }
        if(ans == 0) printf("rainbow\n");
        else printf("freda\n");
    }
    return 0;
}

#include <iostream>
#include <stdio.h>
#include <string.h>
using namespace std;
int dp[250][250];
int getsg(int w,int h){
    if(dp[w][h]!=-1)return dp[w][h];
    bool vis[10000];
    memset(vis,0,sizeof(vis));
    for(int i=2;i<=w-i;i++){//双方采取最优策略进行行动，一定不会剪出1*x或x*1的情况
        dp[i][h]=getsg(i,h);
        dp[w-i][h]=getsg(w-i,h);
        vis[dp[i][h]^dp[w-i][h]]=true;
    }
    for(int i=2;i<=h-i;i++){
        dp[w][i]=getsg(w,i);
        dp[w][h-i]=getsg(w,h-i);
        vis[dp[w][i]^dp[w][h-i]]=true;
    }
    for(int i=0;;i++)
    if(!vis[i])
    return dp[w][h]=i;
}
int main()
{
    int w,h;
    memset(dp,-1,sizeof(dp));
    while(scanf("%d%d",&w,&h)!=EOF){
        if(getsg(w,h))printf("WIN\n");
        else printf("LOSE\n");
    }
    return 0;
}

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#define __ ios::sync_with_stdio(0);cin.tie(0);cout.tie(0)
#define rep(i,a,b) for(int i = a; i <= b; i++)
#define LOG1(x1,x2) cout << x1 << ": " << x2 << endl;
#define LOG2(x1,x2,y1,y2) cout << x1 << ": " << x2 << " , " << y1 << ": " << y2 << endl;
#define LOG3(x1,x2,y1,y2,z1,z2) cout << x1 << ": " << x2 << " , " << y1 << ": " << y2 << " , " << z1 << ": " << z2 << endl;
typedef long long ll;
typedef double db;
const int N = 2000+100;
const int M = 1e5+100;
const db EPS = 1e-9;
using namespace std;

int sg[N],n;

int solve(int x)
{
    if(sg[x] != -1) return sg[x];
    int vis[2000+5]; memset(vis,0,sizeof vis);
    rep(i,1,x){
        int xx = solve(max(0,i-3));
        int yy = solve(max(0,x-i-2));
        vis[xx^yy] = 1;
    }
    rep(i,0,2005) 
        if(vis[i] == 0) return sg[x] = i;
}

int main()
{
    memset(sg,-1,sizeof sg);
    sg[0] = 0;
    scanf("%d",&n);
    if(solve(n) == 0) printf("2\n");
    else printf("1\n");
    return 0;
}

N个结点的有向无环图，图中某些节点上有棋子，两名玩家交替移动棋子。玩家每一步可将任意一颗棋子沿一条有向边移动到另一个点，无法移动者输掉，问先手必胜还是后手必胜

肯定是SG函数求解考虑最终状态 SG[x]=0 (x为出度为0的点)

分析：每一个棋子都是一个独立的子游戏所以答案就是每个棋子所在位置的SG值得异或和

问题变为了求解每个位置的SG值记忆化搜索即可这个题也可以不用记忆化dfs 直接dfs也可

#include <bits/stdc++.h>
using namespace std;
typedef int ll;
inline ll read()
{
    ll s=0;
    bool f=0;
    char ch=' ';
    while(!isdigit(ch))
    {
        f|=(ch=='-'); ch=getchar();
    }
    while(isdigit(ch))
    {
        s=(s<<3)+(s<<1)+(ch^48); ch=getchar();
    }
    return (f)?(-s):(s);
}
#define R(x) x=read()
inline void write(ll x)
{
    if(x<0)
    {
        putchar('-'); x=-x;
    }
    if(x<10)
    {
        putchar(x+'0'); return;
    }
    write(x/10);
    putchar((x%10)+'0');
    return;
}
#define W(x) write(x),putchar(' ')
#define Wl(x) write(x),putchar('\n')
const int N=2005,M=6005;
int n,m,k;
int SG[N];
namespace Picture
{
    int tot=0,Next[M],to[M],head[N];
    inline void add(int x,int y)
    {
        Next[++tot]=head[x];
        to[tot]=y;
        head[x]=tot;
    }
    bool Arr[N];
    inline void dfs(int x)
    {
        if(Arr[x]) return;
        Arr[x]=1;
        int i,Up=0;
        bool Mark[N]={0};
        for(i=head[x];i;i=Next[i])
        {
            dfs(to[i]);
            Up=max(Up,SG[to[i]]);
            Mark[SG[to[i]]]=1;
        }
        for(i=0;i<=Up+1;i++) if(!Mark[i])
        {
            SG[x]=i; break;
        }
    }
    inline void GetSG()
    {
        int i;
        for(i=1;i<=n;i++) if(!Arr[i]) dfs(i);
        return;
    }
}
#define Pc Picture
int main()
{
    int i,ans=0;
    R(n); R(m); R(k);
    for(i=1;i<=m;i++)
    {
        int x=read(),y=read();
        Pc::add(x,y);
    }
    Pc::GetSG();
    for(i=1;i<=k;i++) ans^=SG[read()];
    (ans)?puts("win"):puts("lose");
    return 0;
}

总结一下关于SG函数求解的关键

1.当前状态的SG值是由后继所有状态(除必败状态,因为两个人都足够聪明)的SG值取mex

2.区分后继状态与子游戏子游戏是互不相干的最后答案是所有子游戏的SG值异或和

其他博弈论题：

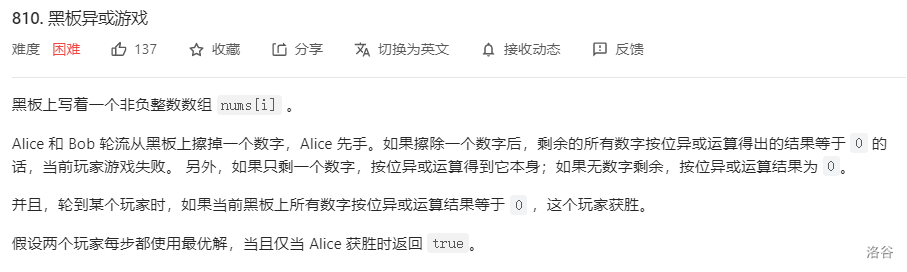
分析：

假设当前所有数的异或和为K

如果K=0 那么先手必胜

如果K≠0 那先手一定必败嘛？

考虑删掉一个数numx 异或和≠0 此时并未处于必败

那要是删掉每一个数num[x] 异或和都是为0呢？这种情况不可能发生

因为如果均为0 只有一种情况就是每个数num[x]均等于K 又因为K≠0 所以不成立

所以此时只要再考虑奇偶性就可以了

综上所诉：如果K=0 或者n为偶数那么先手必胜；如果K≠0并且n为奇数那么后手必胜

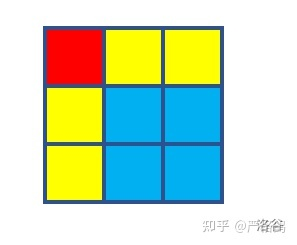
题意：在3*3的格子上玩Nim游戏，特殊的地方是先后手第一次必须全部拿完

我们首先肯定是要枚举先手下的位置。

对于后手，肯定不能选择和先手下的同行同列的，不让就会出现一行里面只有一个还有石子，那么先手直接拿走那个即可。（后手又不傻qwq

那么后手就选择和先手第一个选择的不同行不同列的格子即可。

那么接下来就变成了Nim游戏了。

那么先手的必输态为。

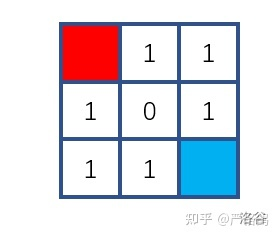
也就是和前两次同行/同列的格子上为1(6个)，不同行同列的为0(1个)。

那么我们可以换成6个a[i]-1,和一个 a[i]的Nim游戏，判断异或和即可。

void slove() {
    int ans = 0;
    for (int i = 1; i <= 3; i++)for (int j = 1; j <= 3; j++)cin >> a[i][j];
    for (int xa = 1; xa <= 3; xa++)for (int ya = 1; ya <= 3; ya++) {
        bool flag = 1;
        for (int xb = 1; xb <= 3; xb++)for (int yb = 1; yb <= 3; yb++) {
            if (xb != xa && yb != ya) {
                int res = 0;
                for (int i = 1; i <= 3; i++)for(int j = 1; j <= 3; j++) {
                    if (i == xa && j == ya)continue;
                    if (i == xb && j == yb)continue;
                    if (i != xa && i != xb && j != ya && j != yb)res ^= a[i][j];
                    else res ^= (a[i][j] - 1);
                }
                if (res == 0)flag = 0;
            }
        }
        ans += flag;
    }
    cout << ans << endl;
}

二分图博弈

这里讲的很详细：https://zhuanlan.zhihu.com/p/555764217

有个例题：https://www.luogu.com.cn/problem/P4055

题意

在一个 n*m的有障碍方阵中，两个人轮流移动棋子走到相邻的方格。

先手决定棋子的初始位置。

最后移动棋子的玩家获胜。

问先手是否有必胜策略，如果有，输出所有能获胜的棋子初始位置。

分析：

看到这种向相邻方格移动棋子的题，很容易想到黑白染色建二分图。

相邻的方格只要没有障碍，就连一条双向边。

每次操作可以转换为从左部走到右部或从右部走到左部。

那么，如果这个二分图是完全匹配，无论先手选哪个点，后手都会选最大匹配中这个点对应的点。

因此这时后手有必胜策略。

如果这个图不是完全匹配，一定有一个点剩下来，也就是最大匹配不需要的点。

先手只要一开始把棋子放在这个点，后手无论怎么走，走到的点都在最大匹配内。

于是后手就变成了第一种情况的先手，先手使用上面后手的策略。

因此这时先手有必胜策略。

因为最大匹配方案不止一种，所以所有最大匹配方案剩下的点都可以作为棋子的初始位置。

但是枚举每种方案的时间复杂度太大了。

我们可以先任意求一种方案，设剩下的点为 ii。

从 i 开始遍历二分图，假设 ii 有一条边一个异侧点 j，j 有一条在已求方案内的边连 i 的同侧点 k，那么一定可以不选 j 到 k 这条边，改选 i 到 j 的边。

k 即改选后的方案剩下的点。

按照到现在为止的思路写就可以 AC 这道题。

但是当我看到讨论区的这个帖子后，发现我没有考虑图不连通的情况。然而造数据的人貌似也没有考虑。

其实很好解决，每个连通块都建一遍图就行。为了方便，我用了 dfs 建图。

#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <queue>
#define rep(i,st,ed) for (int i=st;i<=ed;++i)
#define fill(x,t) memset(x,t,sizeof(x))
using std:: min;
std:: queue<int> que;
const int INF=0x3f3f3f3f;
const int L=205;
const int N=80005;
const int E=640005;
struct edge{int x,y,w,next;}e[E];
int dis[N],rc[L][L],vis[N],bel[N],chs[N];
int cur[N],ls[N],n,m,edCnt=1;
int dx[4][2]={{-1,0},{1,0},{0,-1},{0,1}};
bool flag=false;
char str[L];
void addEdge(int x,int y,int w) {
    e[++edCnt]=(edge){x,y,w,ls[x]}; ls[x]=edCnt;
    e[++edCnt]=(edge){y,x,0,ls[y]}; ls[y]=edCnt;
    // printf("%d %d %d\n", x,y,w);
}
int get_pos(int x,int y) {return (x-1)*m+y;}
int bfs(int st,int ed) {
    while (!que.empty()) que.pop();
    que.push(st);
    rep(i,st,ed) dis[i]=-1; dis[st]=1;
    while (!que.empty()) {
        int now=que.front(); que.pop();
        for (int i=ls[now];i;i=e[i].next) {
            if (e[i].w>0&&dis[e[i].y]==-1) {
                dis[e[i].y]=dis[now]+1;
                if (e[i].y==ed) return 1;
                que.push(e[i].y);
            }
        }
    }
    return 0;
}
int find(int now,int ed,int mn) {
    if (now==ed||!mn) return mn;
    int ret=0;
    for (int &i=cur[now];i;i=e[i].next) {
        if (e[i].w>0&&dis[now]+1==dis[e[i].y]) {
            int d=find(e[i].y,ed,min(mn-ret,e[i].w));
            ret+=d; e[i].w-=d; e[i^1].w+=d;
            if (ret==mn) break;
        }
    }
    return ret;
}
int dinic(int st,int ed) {
    int ret=0;
    while (bfs(st,ed)) {
        rep(i,st,ed) cur[i]=ls[i];
        ret+=find(st,ed,INF);
    }
    return ret;
}
void dfs(int now,int lim) {
    if (vis[now]) return ;
    vis[now]=1;
    if (bel[now]==lim) {
        chs[now]=1;
        flag=true;
    }
    for (int i=ls[now];i;i=e[i].next) {
        if (e[i].w==lim) dfs(e[i].y,lim);
    }
}
int main(void) {
    scanf("%d%d",&n,&m);
    rep(i,1,n) {
        scanf("%s",str);
        rep(j,1,m) if (str[j-1]=='#') rc[i][j]=1;
    }
    rep(i,1,n) rep(j,1,m) {
        int now=get_pos(i,j);
        if (((i^j)&1)&&!rc[i][j]) {
            bel[now]=1;
            addEdge(0,now,1);
            rep(k,0,3) {
                int p=i+dx[k][0],q=j+dx[k][1];
                if (p>0&&p<=n&&q>0&&q<=m&&!rc[p][q]) addEdge(now,get_pos(p,q),1);
            }
        } else if (!((i^j)&1)&&!rc[i][j]) {
            addEdge(now,n*m+1,1);
        }
    }
    int mxFlow=dinic(0,n*m+1);
    dfs(0,1); fill(vis,0);
    dfs(n*m+1,0);
    if (flag) {
        puts("WIN");
        rep(i,1,n) rep(j,1,m) {
            if (chs[get_pos(i,j)]) {
                printf("%d %d\n", i,j);
            }
        }
    } else puts("LOSE");
    return 0;
}

https://www.luogu.com.cn/problem/P4136

分析：

很明显的二分图博弈我们将方格里面的点根据奇偶性分为黑点和白点

发现只要为偶数二分图一定是完美匹配这样先手必胜

奇数就不是完美匹配第一个点就是非匹配点这样先手先操作后手就形成了必胜状态

#include <bits/stdc++.h>
using namespace std;
#define int long long
int a[1000005];
int b[1000005];
signed main(){
	int n;
	while(cin>>n and n){
		if(n%2==0)cout<<"Alice"<<endl;
		else cout<<"Bob"<<endl;
	}
    return 0;
}

posted @ 2019-10-16 20:29 wzx_believer 阅读(302) 评论(0) 编辑收藏举报

刷新页面返回顶部

wzxbeliever

浅谈博弈论

引言

一：巴什博弈

二：尼姆博弈(Nimm Game)

三.SG函数

总结一下关于SG函数求解的关键

1.当前状态的SG值是由后继所有状态(除必败状态,因为两个人都足够聪明)的SG值取mex

2.区分后继状态与子游戏子游戏是互不相干的最后答案是所有子游戏的SG值异或和

综上所诉：如果K=0 或者n为偶数那么先手必胜；如果K≠0并且n为奇数那么后手必胜

公告

wzxbeliever

浅谈博弈论

引言

一：巴什博弈

二：尼姆博弈(Nimm Game)

三.SG函数

总结一下关于SG函数求解的关键

1.当前状态的SG值是由后继所有状态(除必败状态,因为两个人都足够聪明)的SG值取mex

2.区分后继状态与子游戏 子游戏是互不相干的 最后答案是所有子游戏的SG值异或和

综上所诉：如果K=0 或者n为偶数 那么先手必胜；如果K≠0并且n为奇数 那么后手必胜

公告

2.区分后继状态与子游戏子游戏是互不相干的最后答案是所有子游戏的SG值异或和

综上所诉：如果K=0 或者n为偶数那么先手必胜；如果K≠0并且n为奇数那么后手必胜