浅谈概率期望的一些例题

例题一

题意：给定 n种物品，每次购买会随机买到一种，询问买到 n 种物品的期望次数。

考虑我们已经买到了 k 种物品，再继续买多少次能得到第 k+1种物品。

分析
设它为 x，则：
x=(1−k/n)⋅(x+1)+k/n

整理得：
x=1/(1−k/n)=n/(n-k)

那么答案就是 n*(1/n+1/n-1+1/n-2+....+1/1)

例题二

题意：一个软件有 s 个子系统，会产生 n 种bug。某人每天发现一个bug，每个bug属于某个子系统的概率是 1/s ，属于某种分类的概率是 1/n 。问发现n 种bug，且每个子系统都发现bug的天数的期望。

分析：

设 f[i,j] 表示已经找到了 i 种分类，j 种bug，还需要的期望天数。

类比例题一

f[i,j]=f[i,j+1]×i/n×(s-j)/s

+f[i+1,j]×(n-i)/n×j/s

+f[i+1,j+1]×(n-i)/n×(s-j)/s

+f[i,j]×i/n×j/s+1

不要看式子长其实很好理解的

为什么要加一呢，因为你做出这个决策会消耗一

例题三

题意：初始有 k 只生物，这种生物只能活一天，死的时候有 pi 的概率产生 i只新生物（也只能活一天），询问 m 天后所有生物都死的概率（包括 m 天前死的情况）。

分析

首先观察到每只生物是独立的，所以我们可以分开计算，最后 k次方。

例题四

分析：

类比例题二

同样可以得出这样一个dp

f[i,j]表示还有i张红牌(价值+1),选了j张黑牌(价值-1)的得分期望

因为要在最优策略下所以可以得出

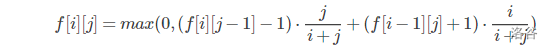
例题五：

主要是这个优化真的好

code：

#include<bits/stdc++.h>
using namespace std;
const int N=1005;
int n,m,l,r,v,a[N];
double dp[N][N<<1];
inline void cmax(double &x,double y) {
	x=(x>y?x:y);
}
int main()
{
	freopen("pigeon.in","r",stdin);
	freopen("pigeon.out","w",stdout);
	scanf("%d%d%d%d%d",&n,&m,&l,&r,&v),dp[n+1][m]=v;
	for(int i=1; i<=n; ++i) scanf("%d",&a[i]);
	for(int i=n; i>=1; i--)
	{
		double sum=0;
		for(int j=l; j<=r; ++j) sum+=dp[i+1][min(j,m)]/(r-l+1);
		for(int j=0; j<=m; ++j) cmax(dp[i][j],dp[i+1][j]+a[i]),cmax(dp[i][j],sum),sum=sum-dp[i+1][min(j+l,m)]/(r-l+1)+dp[i+1][min(j+r+1,m)]/(r-l+1);

	}
    cout<<dp[1][0];
    return 0;	
}