概率期望训练之一

solution by jklover%%%

为什么要写两个转移方程呢？

因为一个是O（N^2）的

如果联立之后呢？

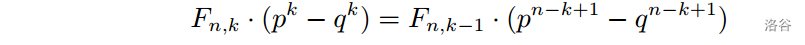
O（N）的

code by std：

#include <cstdio>
using ll = long long;
constexpr int MOD = 998244353;
inline int quick_pow(int a, int n)
{
	int res = 1;
	while (n)
	{
		if (n & 1)
			res = (ll)res * a % MOD;
		a = (ll)a * a % MOD;
		n >>= 1;
	}
	return res;
}
int fact[1000005], inv[1000005], ans[1000005];
inline int binom(int n, int m)
{ return (ll)fact[n] * inv[m] % MOD * inv[n - m] % MOD; }
int main()
{
	int n, a, b;
	scanf("%d%d%d", &n, &a, &b);
	fact[0] = 1;
	for (int i = 1; i <= n; i++)
		fact[i] = (ll)fact[i - 1] * i % MOD;
	inv[n] = quick_pow(fact[n], MOD - 2);
	for (int i = n; i; i--)
		inv[i - 1] = (ll)inv[i] * i % MOD;
	int p = (ll)a * quick_pow(b, MOD - 2) % MOD,
		q = (1 - p + MOD) % MOD, out = 0;
	auto func = [&] (int x) { return (quick_pow(p, x) - quick_pow(q, x) + MOD) % MOD; };
	ans[0] = 1;
	for (int i = 1, cur = 1; i < n; i++, cur = ((ll)cur * cur + 2) % MOD)
	{
		if (a * 2 == b)
			ans[i] = (ll)binom(n, i) * quick_pow(p, (ll)i * (n - i) % (MOD - 1)) % MOD;
		else
			ans[i] = (ll)ans[i - 1] * func(n - i + 1) % MOD *
					 quick_pow(func(i), MOD - 2) % MOD;
		out = (out + (ll)ans[i] * cur) % MOD;
	}
	printf("%d\n", out);
	return 0;
}