数论学习之二

https://www.luogu.org/problem/P1313

题目描述

给定一个多项式(by+ax)^{k，请求出多项式展开后x}n* y^m项的系数。

如果你不知道二项式定理，可以手推一下，发现这系数是杨辉三角（noip2017D1T1）

因为数据比较小，所以直接用f[i,j]=f[i,j-1]+f[i-1,j-1]推出来

如果你知道二项式定理；

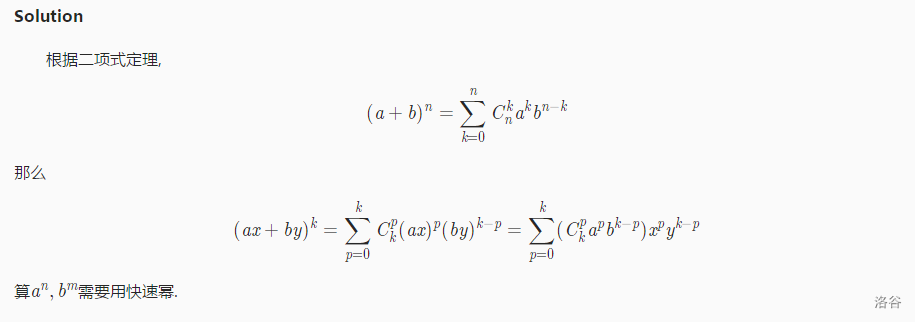
于是就完了；

code：

#include<iostream>
using namespace std;
const int mo = 10007;
const int maxn = 1007;
//给定一个多项式(by+ax)^k，请求出多项式展开后x^n*y^m 项的系数。
int a,b,k,n,m;
int C[maxn][maxn];
int getksm(int a,int b)
{
    int base = a,ans = 1;
    while (b)
    {
        if (b & 1) ans = (ans*base) %mo;
        base = (base*base) %mo;
        b>>=1;    
    }
    return ans;
}
int main()
{
    cin>>a>>b>>k>>n>>m;
    a %= mo; b %= mo;
    a = getksm(a,n);
    b = getksm(b,m);
    for (int i = 1; i<=k; i++)
    {
        C[i][0] = 1;
        C[i][i] = 1;
    }
    int p = min(n,m);
    for (int i = 2; i<=k; i++)//从1开始就会WA
    {
        for (int j = 1; j<=p; j++)
        {
            C[i][j] = (C[i-1][j]+C[i-1][j-1]) %mo;
        }
    }
    int ans = (a*b) % mo;
    ans = (ans * C[k][p]) % mo;
    cout<<ans<<endl;
    return 0;
}