凸包-Graham扫描法

凸包

简介

凸包 \(（Convex Hull）\) 是一个计算几何（图形学）中的概念。

在一个实数向量空间\(V\)中，对于给定集合\(X\)，所有包含X的凸集的交集\(S\)被称为\(X\)的凸包。\(X\)的凸包可以用\(X\)内所有点\((X1，...Xn)\)的凸组合来构造.

在二维欧几里得空间中，凸包可想象为一条刚好包著所有点的橡皮圈。

用不严谨的话来讲，给定二维平面上的点集，凸包就是将最外层的点连接起来构成的凸多边形，它能包含点集中所有的点。

性质

凸包用最小的周长围住了给定的所有点；

如果一个凹多边形围住了所有的点，它的周长一定不是最小；

如下图。根据三角不等式，凸多边形在周长上一定是最优的；

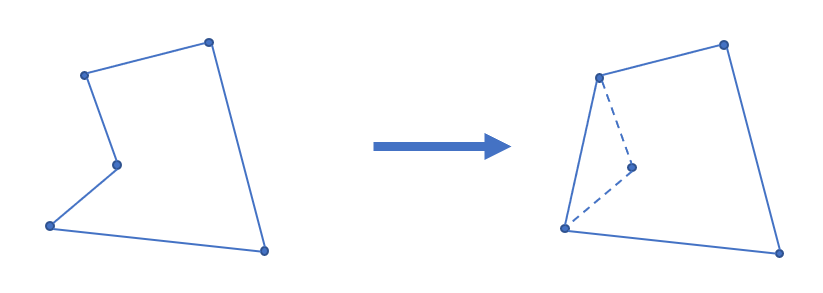
前置知识

叉积

两个向量 \(A(x1,y1)\) , \(B(x2,y2)\)

的叉积为 \(x1 \times y2−x2 \times y1x1 \times y2−x2 \times y1\) ;

先放出代码

inline ll cross(node p,node a,node b)
{
	ll a1,b1,a2,b2;
	a1=a.x-p.x; b1=a.y-p.y;
	a2=b.x-p.x; b2=b.y-p.y;
	return a1*b2-a2*b1;
}

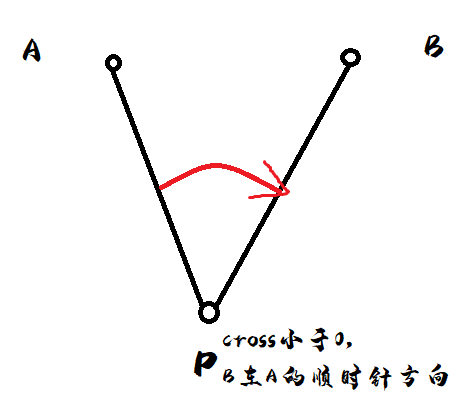
对于这个函数如果函数值为正数说明，\(B\) 在 \(A\) 的逆时针方向；

如果函数值为负数说明，\(B\) 在 \(A\) 的顺时针方向；

如果函数值为 \(0\) 说明， \(A\) ,\(B\) ,\(P\) 三点共线；

求三点的三角形面积

\(S= \frac{1}{2} abs((x1−x3) \times (y2−y3)−(x2−x3) \times (y1−y3))\) ;

算法：Graham扫描法

复杂度 : n (log (n)) ;

思路

大概做法是找到一个点，朝一个方向不断加点，保证所有的点在里面并且是一个凸多边形；

具体找到一个纵坐标最小的点作为基点，若有多个则选取横坐标最小的点；

然后以基点为原点构造平面直角坐标系，按每个点到原点的直线与 x 轴的夹角 从小到大排序；

排序可以利用叉积判断点位置关系；

如图

之后利用叉积性质，例如：

栈元素: \(p0\) , \(p1\) ； 利用叉积判断 线段\(p0p1\) 是否在 \(p1p2\) 的逆时针方向； 满足入队；

栈元素: \(p0\) , \(p1\) , \(p2\) ； 判断 线段\(p1p2\) 是否在 \(p2p3\) 的逆时针方向； 不满足 \(p2\) 出队；

。。。。。。

简单来说就是每次去掉那个往内部凹的角;

动图GIF

代码

inline ll cross(node p,node a,node b)//叉积公式 
{
    ll a1,b1,a2,b2;
    a1=a.x-p.x; b1=a.y-p.y;
    a2=b.x-p.x; b2=b.y-p.y;
    return a1*b2-a2*b1;
}
inline ll cmp(node x,node y)
{
    ll sum=cross(p[1],x,y);
    if(sum>0) return 1;//sum 大于零说明，y 在 x 的逆时针方向 
    if(sum<0) return 0;//sum 小于零说明，y 在 x 的顺时针方向 
    return dis(x,p[1])<dis(y,p[1]); //如果三点共线，近的排在前面 
}
inline void convex_hull()
{
    node a=(node){1<<30,1<<30};
    ll id=0;
    for(re ll i=1;i<=n;i++)
    if(p[i].y<a.y||(p[i].y==a.y&&p[i].x<a.x))
    {
        a=p[i];
        id=i;
    }//确定纵坐标最小的基点 
    swap(p[1],p[id]);
    sort(p+2,p+n+1,cmp);//除基点外 排序 
    aa[++top]=p[1];
    aa[++top]=p[2];
    for(re ll i=3;i<=n;i++)
    {
        while(top>1&&cross(aa[top],aa[top-1],p[i])>=0)//如果出现凹下去的地方 
            top--;    //退栈 
        aa[++top]=p[i];
    }
}