面试题68 - I：二叉搜索树的最近公共祖先（C++）

题目地址：https://leetcode-cn.com/problems/er-cha-sou-suo-shu-de-zui-jin-gong-gong-zu-xian-lcof/

题目描述

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树:  root = [6,2,8,0,4,7,9,null,null,3,5]

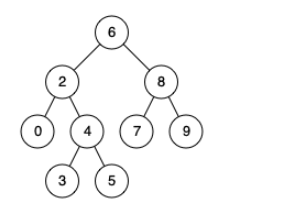
题目示例

示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明:

所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉搜索树中。

解题思路

要理解最近公共祖先，首先要明确祖先的定义，若一个节点cur在另一个节点prev的左右子树，或者节点cur等于节点prev，则节点prev就是节点cur的祖先节点。而最近公共祖先可以表示成，我们假设root是节点p和q的公共祖先节点，如果root的左节点left和右节点right都不是p和q的公共祖先，则root就是节点p和q的最近公共祖先节点。具体来说，如果节点root为最近公共祖先节点，只能是以下几种情况

• 节点p和q在节点root的子树中，而且是节点root的两侧；
• 如果p=root，q则在root的左或右子树中；
• 如果q=root，p则在root的左右子树中；

另外，观察题目给出的树为二叉搜索树以及条件说明，我们可以得出如下的结论

• 若root->val 大于p->val，则节点p在节点root的左子树中；
• 若root->val小于p->val，则节点p在节点root的右子树中；
• 若root->val等于p->val，则节点p和节点root指向同一节点；

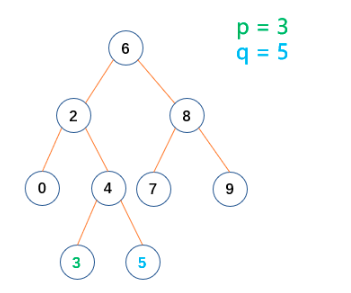
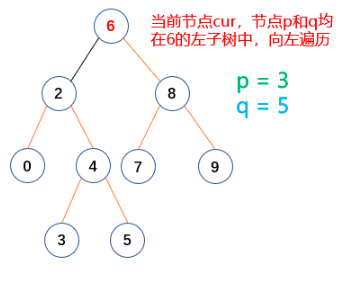
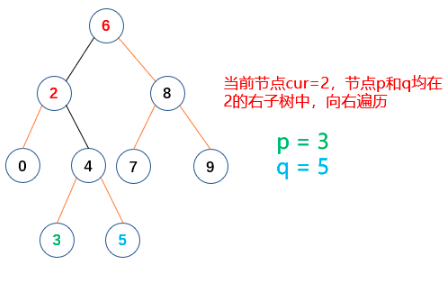
程序源码

非递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        TreeNode* cur = root; //所有节点的值都是唯一的。 p、q 为不同节点且均存在于给定的二叉搜索树中。 根据这两个条件，推出不会有 root == null 的情况出现
        while(cur != nullptr)
        {
            if(cur->val > p->val && cur->val > q->val)
            {
                cur = cur->left; //节点p和节点q均在节点cur的左子树中，继续向左遍历
            }
            else if(cur->val < p->val && cur->val < q->val)
            {
                cur = cur->right; //节点p和节点q均在节点cur的右子树中，继续向右遍历
            }
            else
                break; //节点p和节点q均在节点cur的两侧，跳出循环，找到了最近公共祖先节点cur
        }
        return cur;
    }
};

递归

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root == nullptr) return nullptr;
        if(root->val > p->val && root->val > q->val)
        {
            return lowestCommonAncestor(root->left, p, q);
        }
        if(root->val < p->val && root->val < q->val)
        {
            return lowestCommonAncestor(root->right, p, q);
        }
        return root;
    }
};

参考文章

https://leetcode-cn.com/problems/er-cha-sou-suo-shu-de-zui-jin-gong-gong-zu-xian-lcof/solution/mian-shi-ti-68-i-er-cha-sou-suo-shu-de-zui-jin-g-7/  （动画清晰明了）