数据结构——树和图

图和树与其他数据结构的区别

图是一种特殊的数据结构，要认识图，首先要找出图的特殊性在哪里，即图与其他常见的数据结构的区别。

区别——线性的数据结构与非线性的数据结构

线性结构（常见）

表现形式

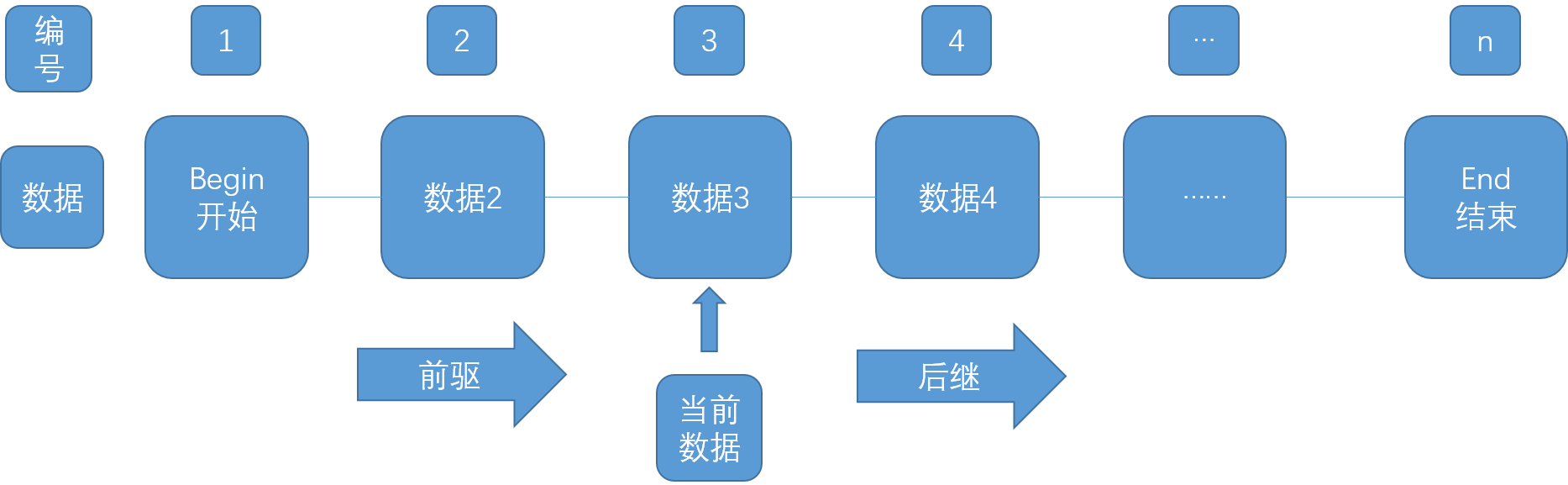
线性的数据结构是指类似数组和链表的数据结构（能够明确的知道前一个数据与下一个数据）。
例如：

我们可以称它（线性结构）是一对一的，对于每一个数据，都只有一个直接前驱和一个直接后继。
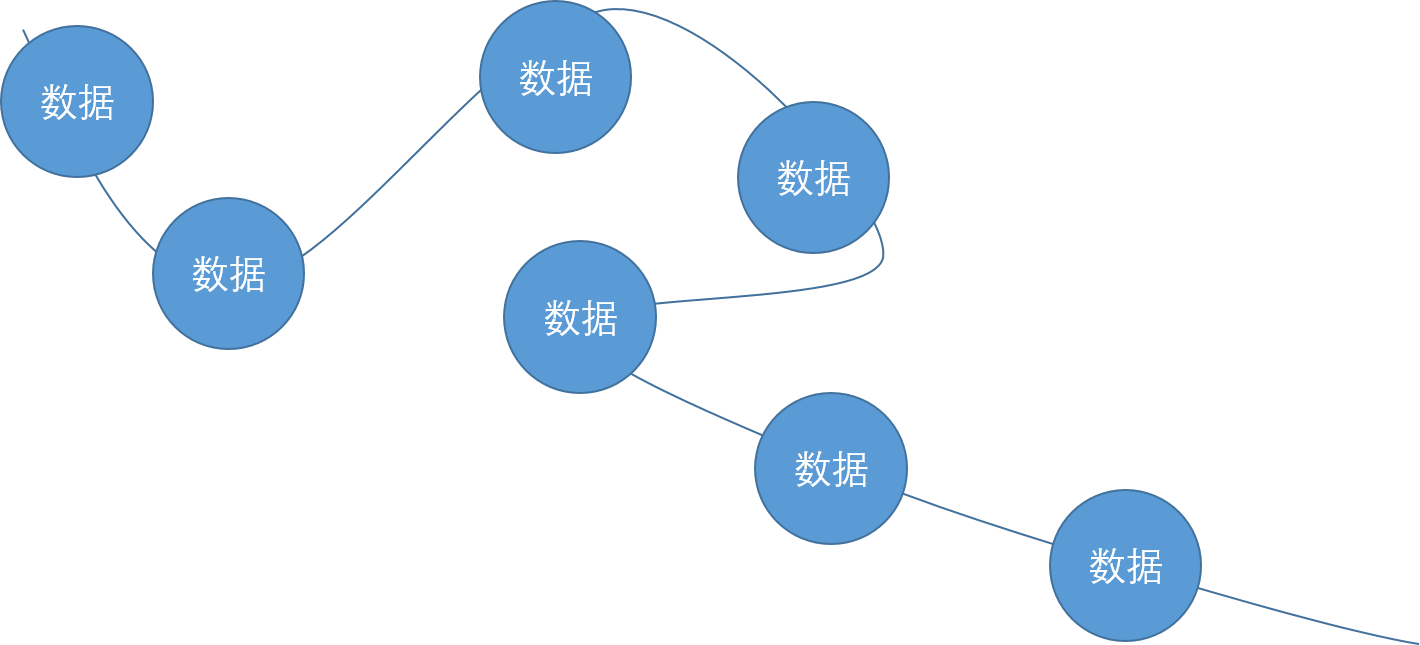
又或者说，他可以表示成能够用一根线串联的数据组：

非线性结构

表现形式

而图与树则是一对多的,故而类似这种结构，我们称它为非线性的数据结构。（当然图也可以是一笔连成的，那样比较特殊，也可以通俗的认为线性表是一种特殊的图）
树：

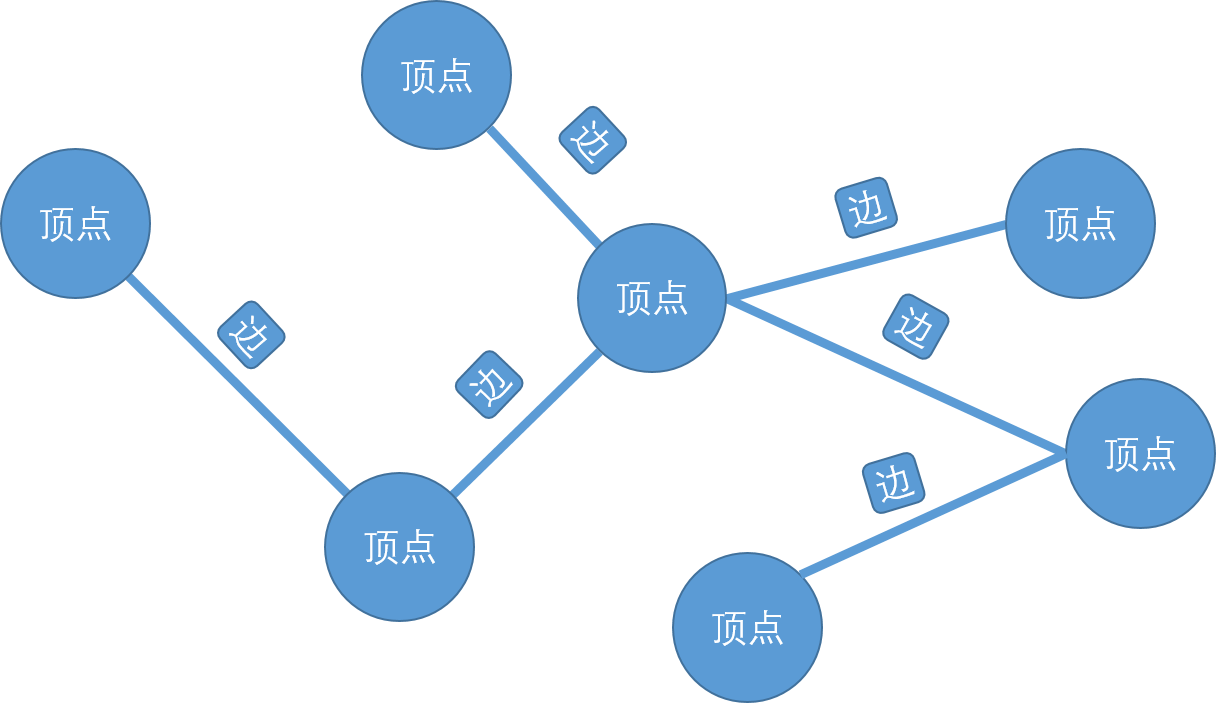
图：

这样的结构在我们生活中是十分常见的。（显而易见的一对多）

生活中的应用

图这种数据类型在生活中非常常见。
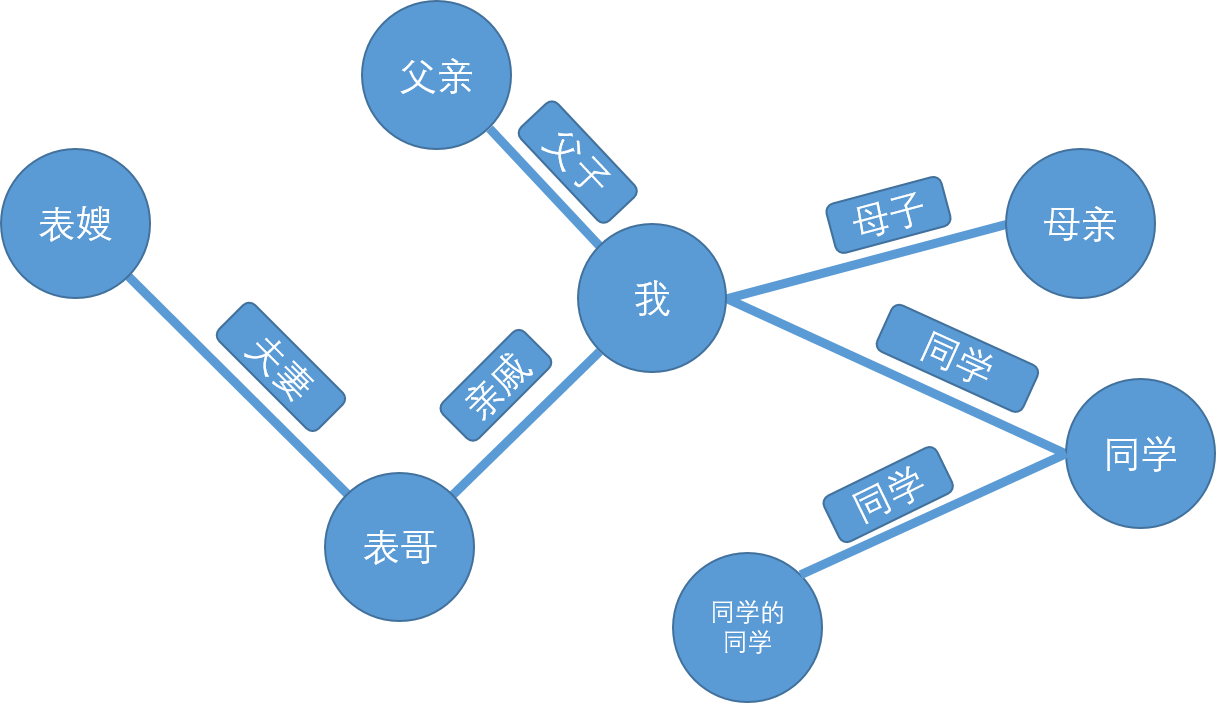
例如，我们将上图的每个顶点视作一个用户，那么每条链接两个用户的边就可以视作两个用户互为好友。
如此，这样就可以简单描述寻找他人的微信好友是如何实现的。

也可以想一想自己和身边的人的关系，是否也是可以用图来描述的?

图的概念

实际上，我们可以将图视作从社会中常见的关系中抽象出来的一种特殊的模型，它既可以考虑到个体（顶点）与个体之间的联系，也可以考虑到顶点内部的特殊性。在基本了解图的特殊性与图在生活中的表现形式后，我们来了解一些关于图的术语。

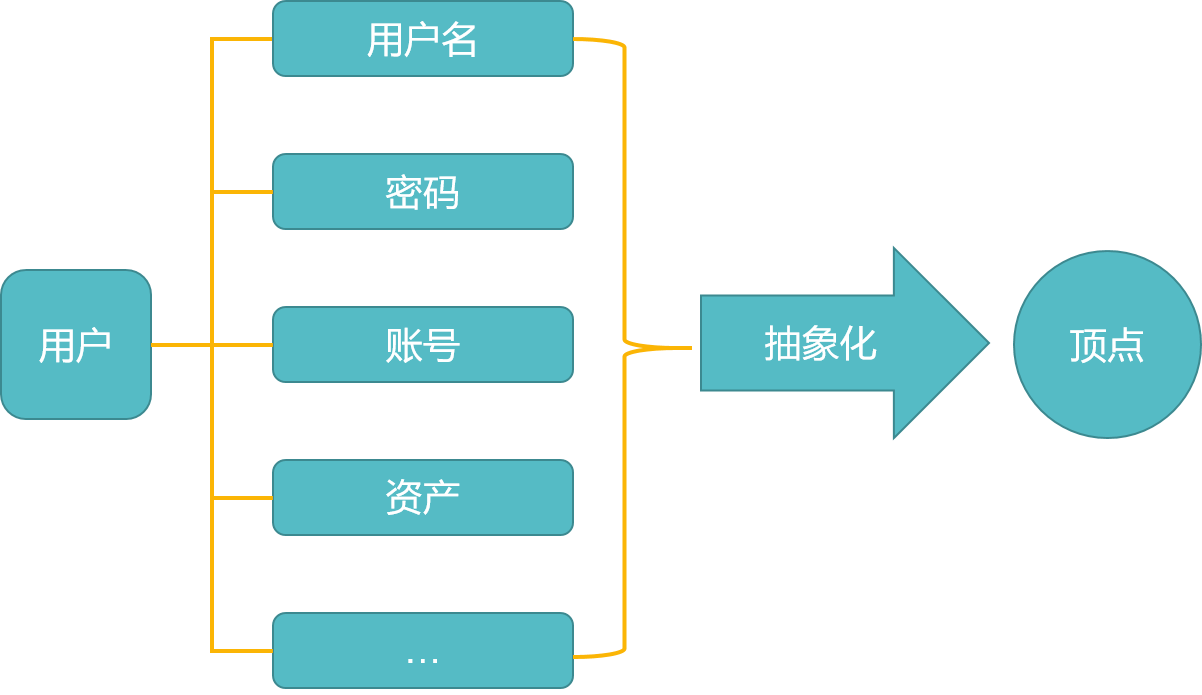
顶点——描述个体的抽象概念

我们可以先简单地将顶点看做是微信中的个人用户。在讨论数据结构的特点时，我们可以忽略特定数据（用户包含用户名、账号、密码等等，我们忽略掉）本身包含的内容，统一视作数据这一抽象概念。
最终，我们脱离微信用户这个特殊的例子，将其抽象化，我们就可以明白，顶点实际上就是描述一系列个体的集合。

边——描述关系的抽象概念

想象两个微信用户（作为两个顶点）若他们互为好友，则我们可以用一条边（线）将顶点连接来表示他俩之间的好友关系。我们从特定的微信用户脱离出来，使其抽象化，让它更具普遍性，这就是图的边了。也就是说，每条边描述的是两个顶点（个体）之间的关系。

有向图与无向图

在实际生活中，两个个体之间的关系可能是单向的（例如：对方开启了好友验证），也可能是双向的。故而，就出现了代表单向关系的有向图，和代表双向关系的无向图。

度、入度、出度——关系的数量

顶点的度、入度和出度

如果把顶点视作微信好友，那么顶点的度就可以视作用户添加的微信好友的数量。再从微信好友中抽象出来，不难理解，“顶点的度”描述的就是某一个体的关系的多寡。

边的度、入度和出度

不难看出，一条边为整个图提供两个度。

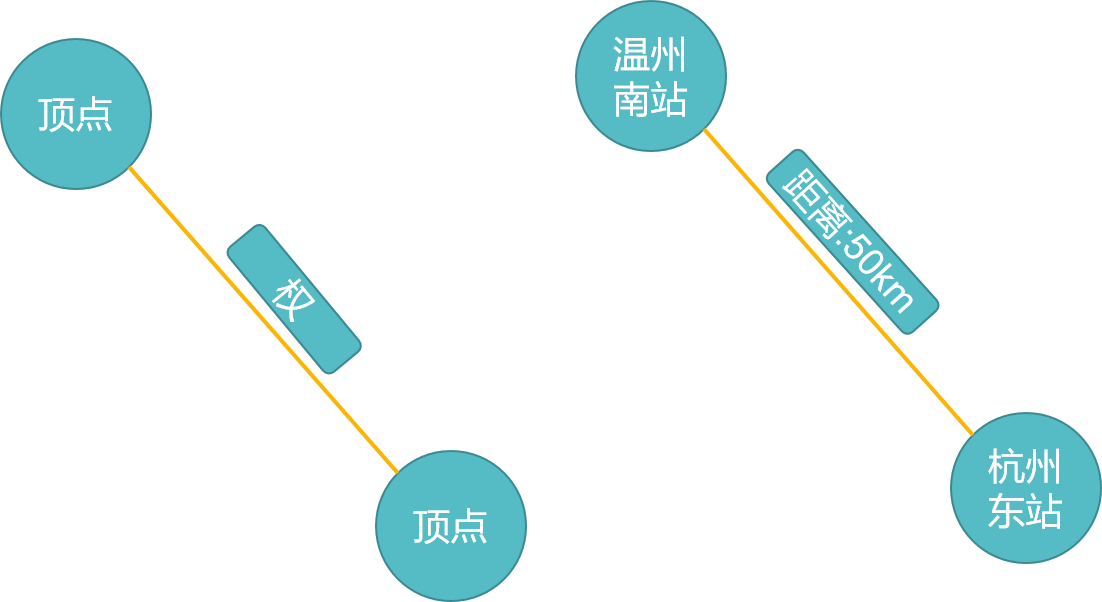
权——关系的性质

边不仅可以表示顶点与顶点（个体与个体）之间是否关联（若关联则为真，不关联则为假）。也可以表示顶点（个体）之间的偏序关系（ 类似\(\leqslant\)这种关系，也就是这种关系让数据之间可以比较 ）有兴趣的话可以了解一下哈斯图怎么画。我们可以寻找一些例子来理解权的概念。比如两个不同的动车站点之间的距离，我们就可以用顶点表示站点，边表示站点连通（可达），边上的权来表示站点间的距离的大小。
为了区分有权的（偏序的）图和没有权的图，我们将边上带权的图称作网。相应的有向图 \(\large\Rightarrow\)有向网，无向图 \(\large\Rightarrow\)无向网。

图的问题应用

一道简单的atcoder题目 ABC-303-B
在生活中判断多边形能否一笔画、寻找起点到目的地的最短路径、判断一个工程竣工的最短时间等都是可以用图的思想解决的。
在2023年6月浙江省技术科目选考卷的最后一题，就是一道判断工程竣工最短时间的AOE网(Activity On Edge)题目。

树的概念

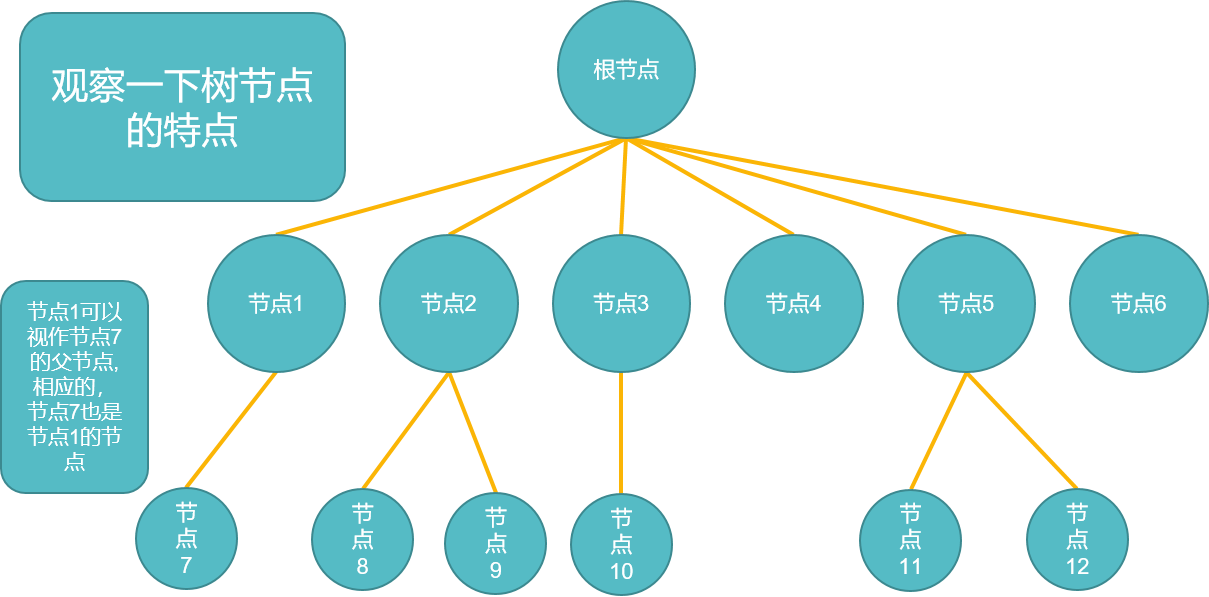
根节点、父节点、子节点、叶子节点

树的定义：在任何一棵非空树中：1. 有且只有一个特定的称为 根（root） 的结点；2. 当n>1时，其余结点可分为m（m>0）个 互不相交 的有限集，其中每一个集合又是一棵树，并且成为 根的子树（subtree）。[看不懂没有关系]

叶子节点(leaf):度为零\(d(v)=0\)的节点，就像树的叶子不会再延伸出枝干一般。

根节点(root):没有父节点的节点，可以说是这棵树开始的地方。

父节点(parent/father):拥有若干子节点的节点，是子节点的上级。

子节点(child):顾名思义，是父节点的衍生。

子树:就是在母树中分离出来的一部分树。

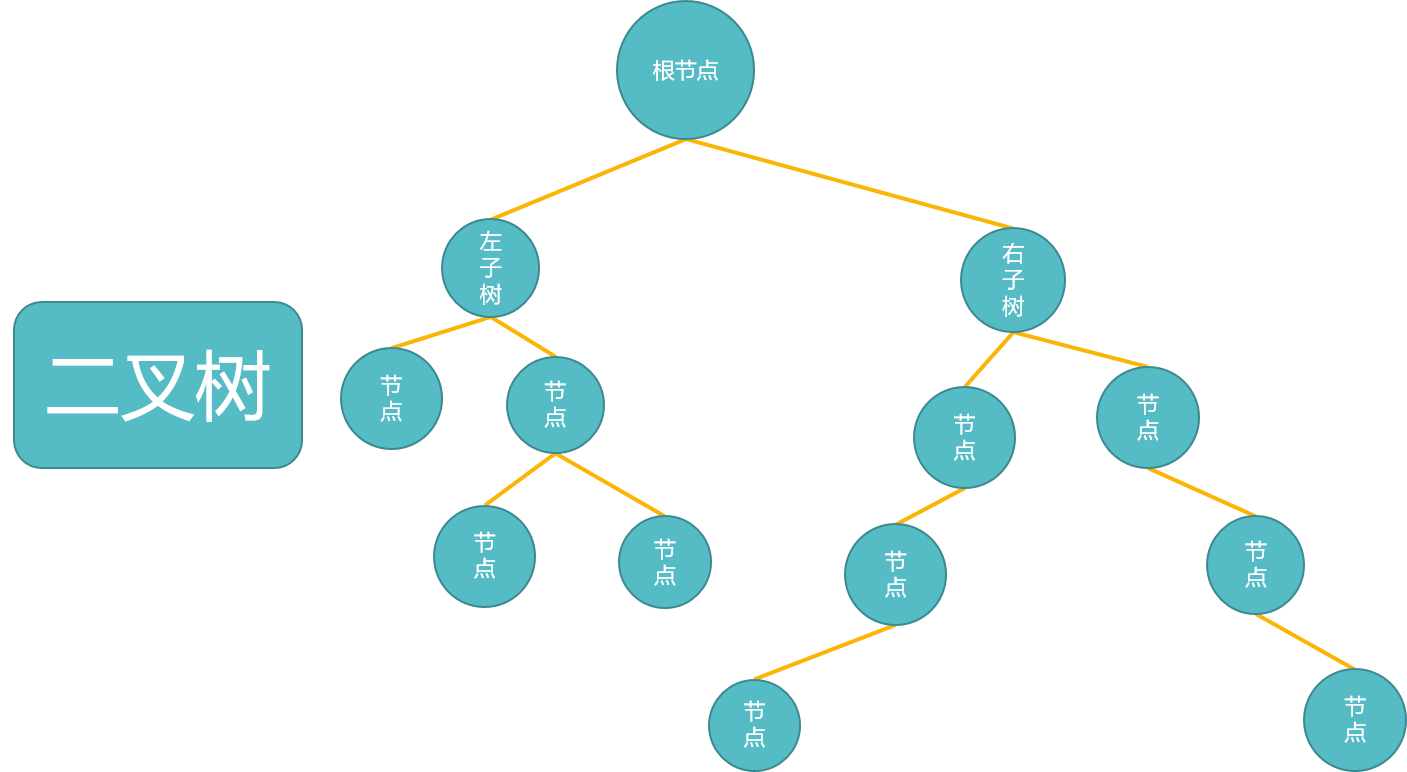
二叉树

上一节我们看的是普通的树，而二叉树就是树中的一种特殊形式。
它和普通树的区别就在于，每个节点最多只有两个子节点

二叉树的简单算法

多观察一下，就会发现，树的每一个节点都可以视作一颗新树的根，这里就可以利用递归的思想了。

名词解释

访问：读取节点中的数据。
遍历：按照一定的顺序访问所有的树。

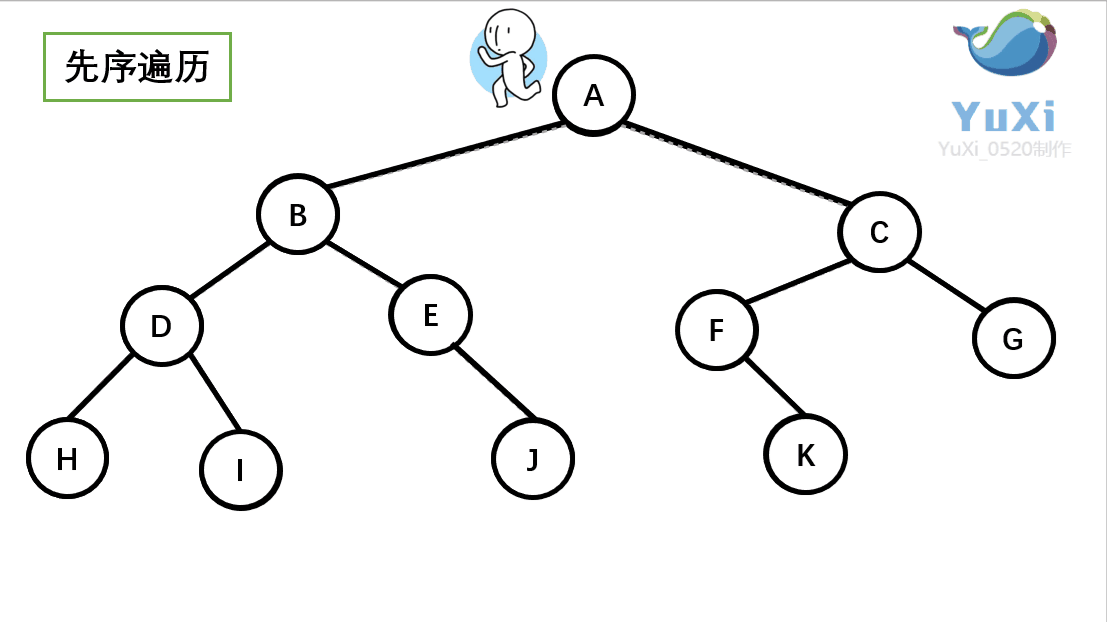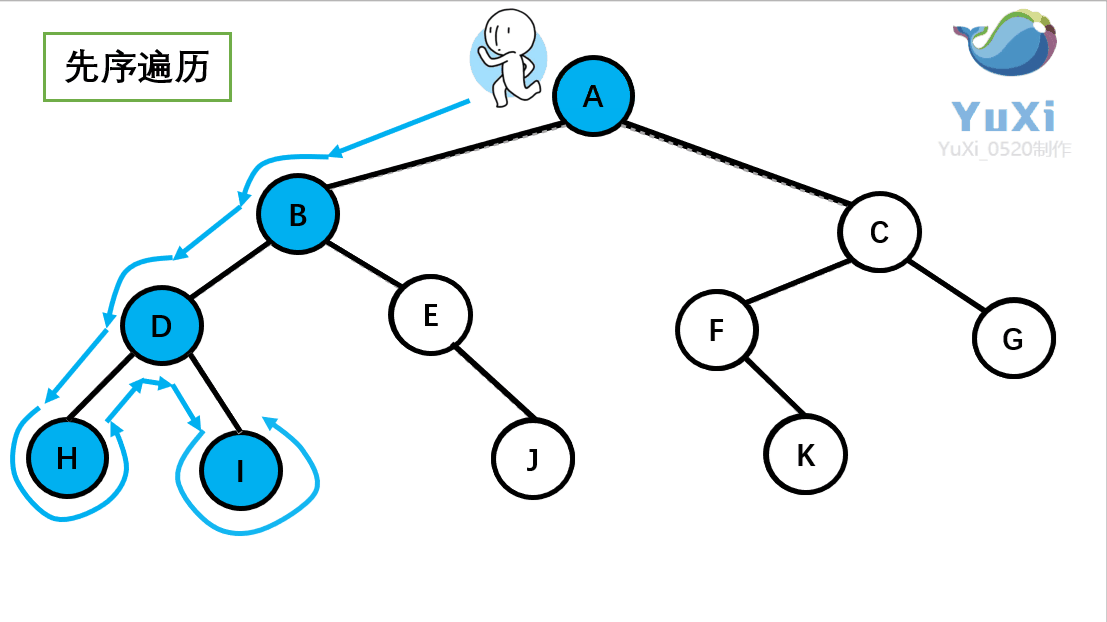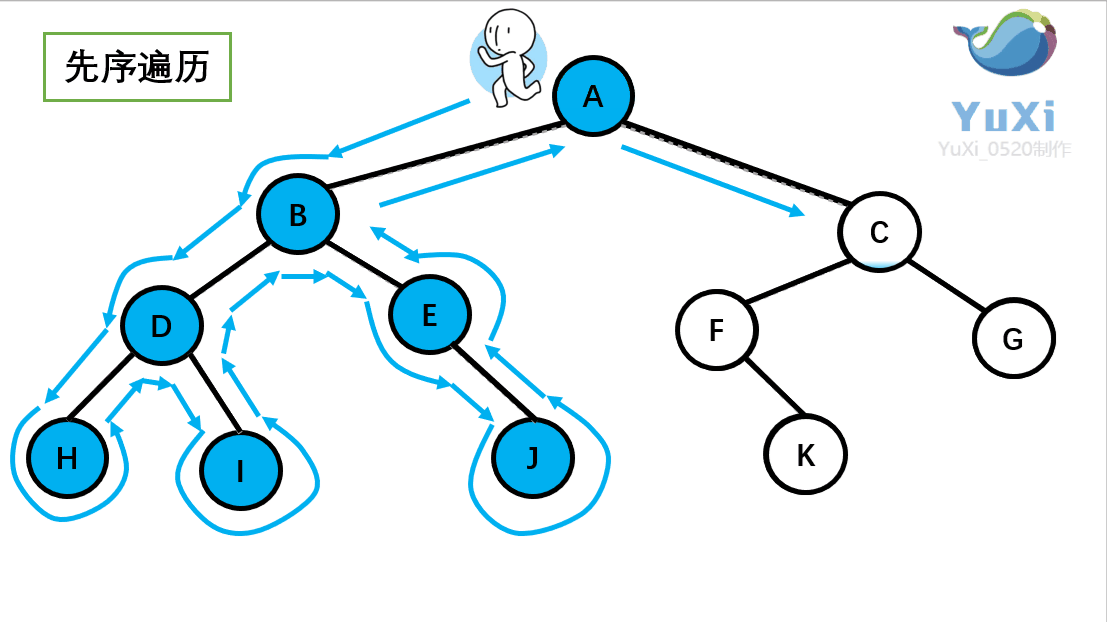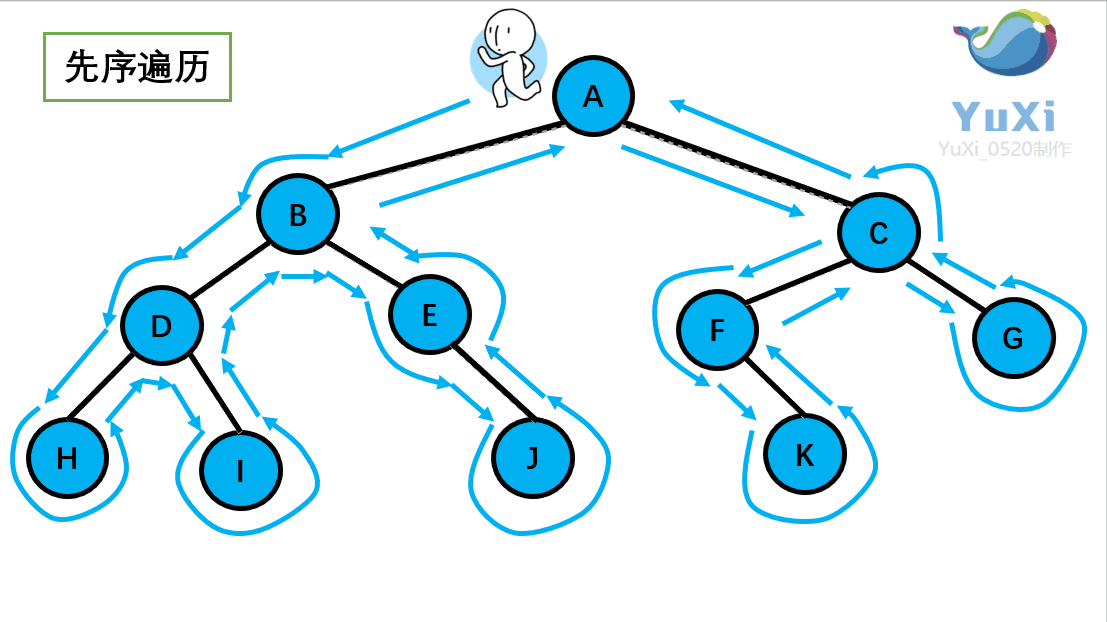
前序遍历

所谓前序遍历，就是先遍历一颗二叉树的根节点，再遍历其左子树，之后再遍历其右子树。即

1. 访问根节点；
2. 找到左子树的根节点，若找到(左子树存在)，则重复步骤1，否则重复步骤3；
3. 找到右子树的根节点，若找到(右子树存在)，则重复步骤1，否则跳到未执行步骤3的最近祖先节点,若该节点不存在，程序结束。

如果觉得难理解，也可以想象为一个小人从一棵二叉树根节点为起点，沿着二叉树外沿，逆时针走一圈回到根节点，路上遇到的元素顺序，就是先序遍历的结果。如果觉得难理解，也可以想象为一个小人从一棵二叉树根节点为起点，沿着二叉树外沿，逆时针走一圈回到根节点，路上遇到的元素顺序，就是先序遍历的结果。
转载至(https://blog.csdn.net/chinesekobe/article/details/110874773?ydreferer=aHR0cHM6Ly9jbi5iaW5nLmNvbS8%3D)

中序遍历

所谓前序遍历，就是先遍历一颗二叉树的左子树，再遍历其根节点，之后再遍历其右子树。即
中序遍历可以看成，二叉树每个节点，垂直方向投影下来（可以理解为每个节点从最左边开始垂直掉到地上），然后从左往右数，得出的结果便是中序遍历的结果。转载至(https://blog.csdn.net/chinesekobe/article/details/110874773?ydreferer=aHR0cHM6Ly9jbi5iaW5nLmNvbS8%3D)

后序遍历

所谓后序遍历，就是先遍历一颗二叉树的左子树，再遍历其右子树，之后再遍历其根节点。
后序遍历就像是是围着树的外围绕一圈，如果发现一剪刀就能剪下的葡萄（必须是一颗葡萄）（也就是葡萄要一个一个掉下来，不能一口气掉超过1个这样），就把它剪下来，组成的就是后序遍历了。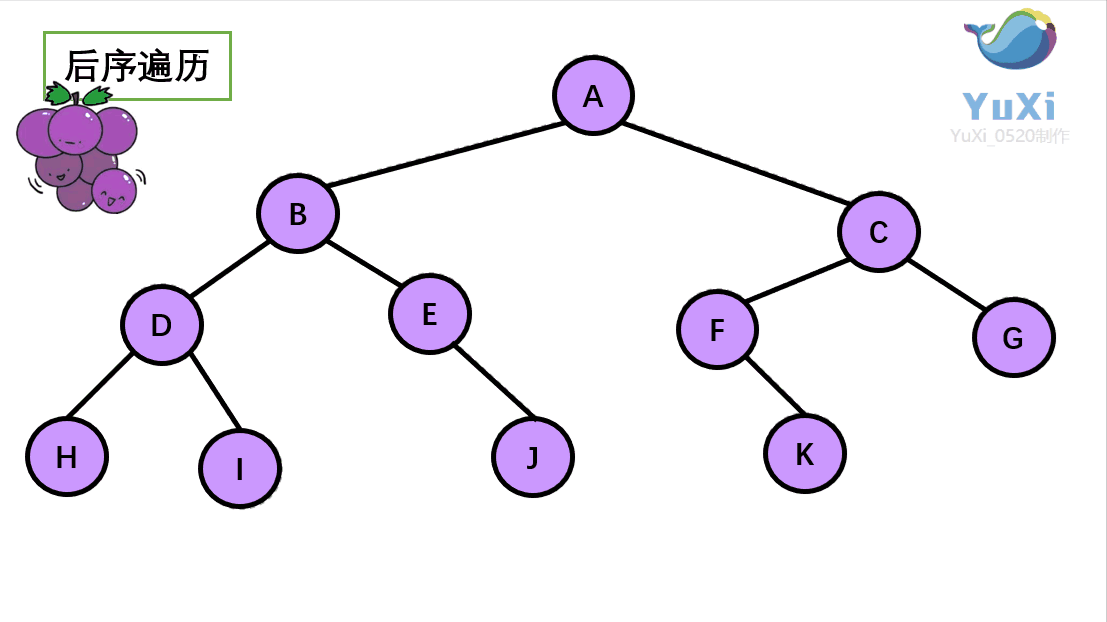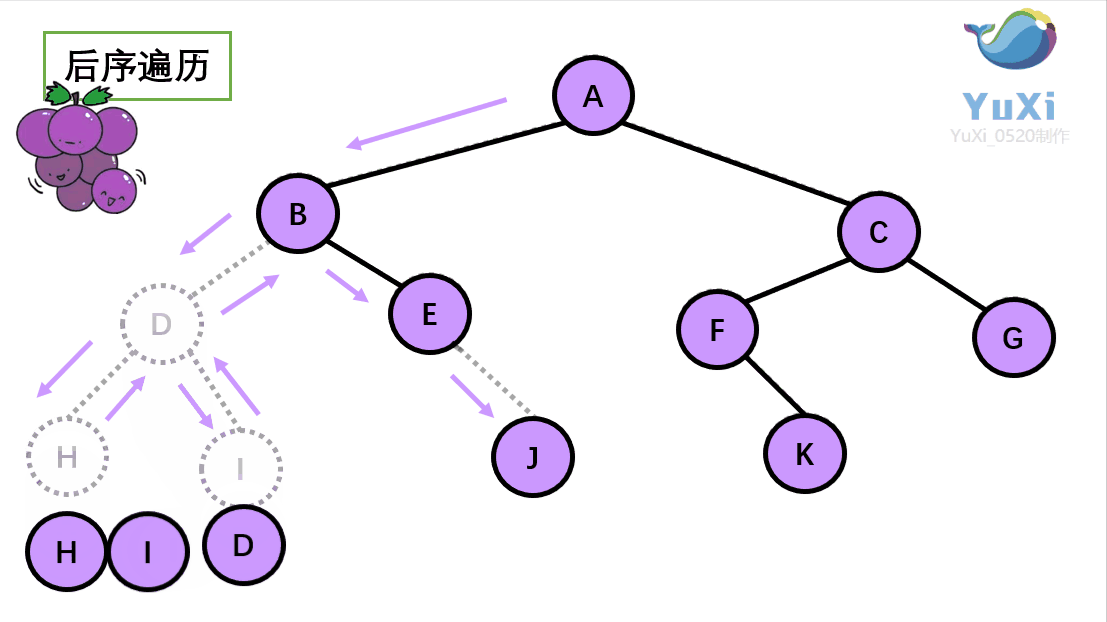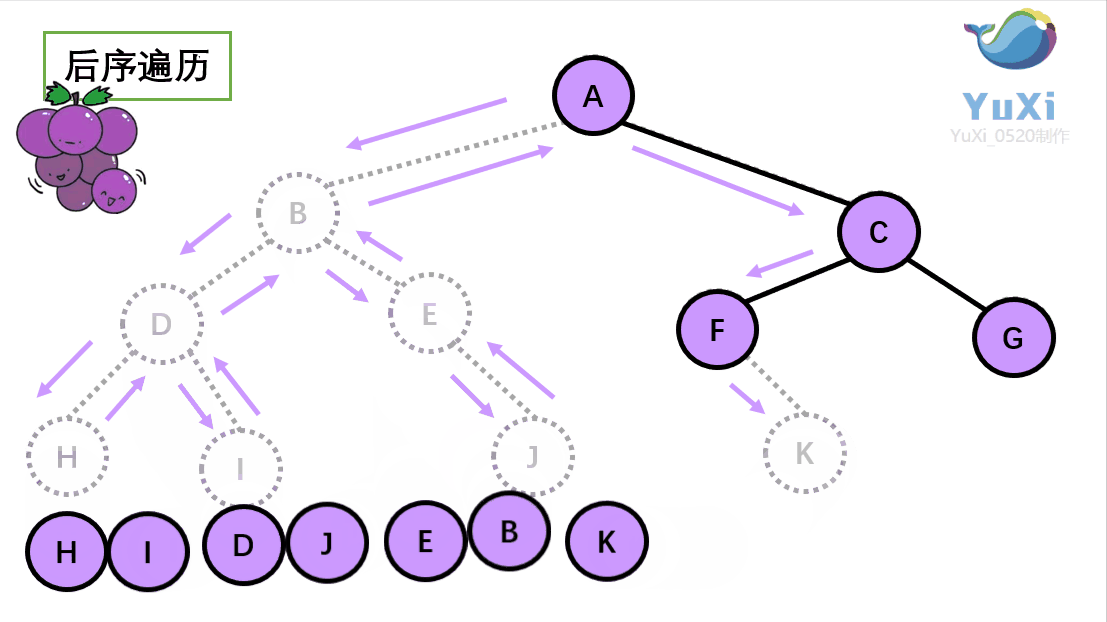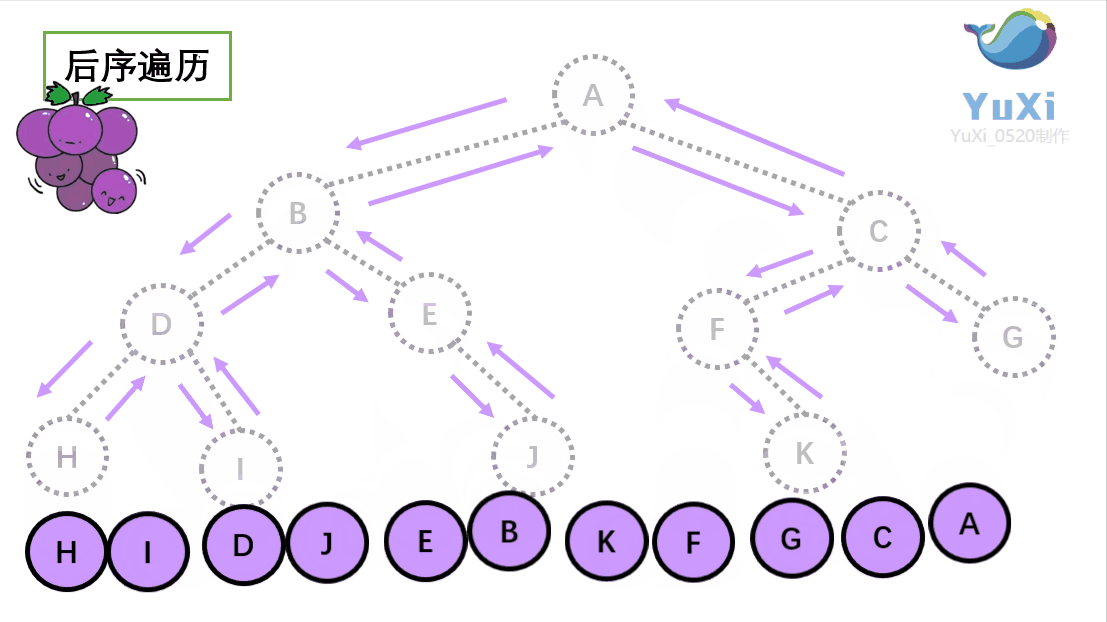转载至(https://blog.csdn.net/chinesekobe/article/details/110874773?ydreferer=aHR0cHM6Ly9jbi5iaW5nLmNvbS8%3D)

层序遍历

最简单，就是按照二叉树的层次，一个一个地访问过去。

树的题目应用

2023年浙江省技术选考第8题。