python 迪克斯特拉（Dijkstra）

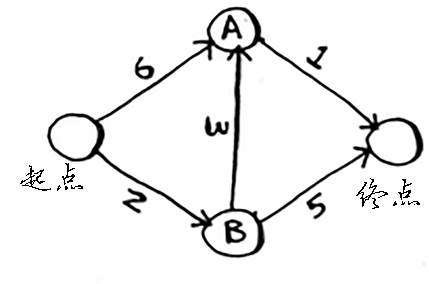
从起点到终点的路径如上图所示，每条路径的长度都不相同（权重），如何从起点找到一条路径，长度最短？

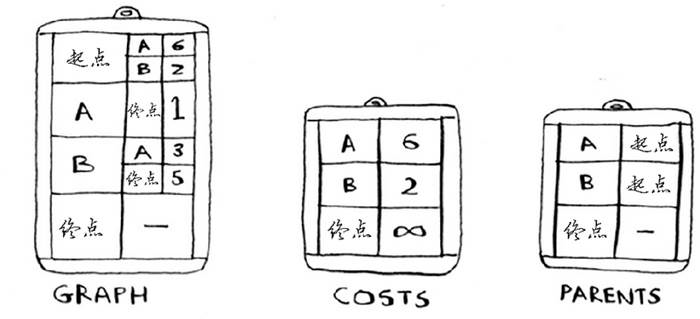
建模：GRAPH存储了整张图的结构；costs存储了从起点开始，到每个点的最短距离（从起点到A是6，但是从 起点-> B -> A 是5，所以后面A的路径其实会变成5）；PARENTS记录了每个地点的父节点，譬如开始时 A 的父节点是 起点，但是从 起点->B->A 更近，所以 A 的父节点会变成 B）

graph ={}

graph['start'] = {}
graph['start']['a'] = 6
graph['start']['b'] = 2

graph["a"] = {}
graph["a"]["fin"] = 1

graph["b"] = {}
graph["b"]["a"] = 3
graph["b"]["fin"] = 5

graph["fin"] = {} 

infinity = float("inf")


costs = {}
costs["a"] = 6
costs["b"] = 2
costs["fin"] = infinity

parents = {}
parents["a"] = "start"
parents["b"] = "start"
parents["fin"] = None
processed = []

def find_lowest_cost_node(costs):
    lowest_cost = float("inf")
    lowest_cost_node = None
    for node in costs: # 遍历所有的节点
        cost = costs[node]
        if cost < lowest_cost and node not in processed: # 如果当前节点的开销更低且未处理过，
            lowest_cost = cost  # 就将其视为开销最低的节点
            lowest_cost_node = node
    return lowest_cost_node

node = find_lowest_cost_node(costs)  # 在未处理的节点中找出开销最小的节点


while node is not None:  # 这个while循环在所有节点都被处理过后结束
    print('\n花费节点：',costs)
    cost = costs[node]
    print('最低花费节点：%s , 花费:' % node,cost)
    neighbors = graph[node]
    
    for n in neighbors.keys():  # 遍历当前节点的所有邻居
        new_cost = cost + neighbors[n]
        print('邻居：',neighbors)
        print('邻居：',n,'总花费:',new_cost)
        print('%s 原本花费'%n,costs[n])
        if costs[n] > new_cost:  # 如果经当前节点前往该邻居更近，
            costs[n] = new_cost  # 就更新该邻居的开销
            parents[n] = node  # 同时将该邻居的父节点设置为当前节点
            print('%s cost -> %s , parents -> %s' %(n,new_cost,node))
        else:
            print('%s 原本的费用更小，不用改'%n)
    processed.append(node)  # 将当前节点标记为处理过
    node = find_lowest_cost_node(costs)  # 找出接下来要处理的节点，并循环

print(costs["fin"])