CF287-C

C. Guess Your Way Out!

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Amr bought a new video game "Guess Your Way Out!". The goal of the game is to find an exit from the maze that looks like a perfect binary tree of height h. The player is initially standing at the root of the tree and the exit from the tree is located at some leaf node.

Let's index all the leaf nodes from the left to the right from 1 to 2^h. The exit is located at some node n where 1 ≤ n ≤ 2^h, the player doesn't know where the exit is so he has to guess his way out!

Amr follows simple algorithm to choose the path. Let's consider infinite command string "LRLRLRLRL..." (consisting of alternating characters 'L' and 'R'). Amr sequentially executes the characters of the string using following rules:

• Character 'L' means "go to the left child of the current node";
• Character 'R' means "go to the right child of the current node";
• If the destination node is already visited, Amr skips current command, otherwise he moves to the destination node;
• If Amr skipped two consecutive commands, he goes back to the parent of the current node before executing next command;
• If he reached a leaf node that is not the exit, he returns to the parent of the current node;
• If he reaches an exit, the game is finished.

Now Amr wonders, if he follows this algorithm, how many nodes he is going to visit before reaching the exit?

Input

Input consists of two integers h, n (1 ≤ h ≤ 50, 1 ≤ n ≤ 2^h).

Output

Output a single integer representing the number of nodes (excluding the exit node) Amr is going to visit before reaching the exit by following this algorithm.

Sample test(s)

input

1 2

output

2

input

2 3

output

5

input

3 6

output

10

input

10 1024

output

2046

Note

A perfect binary tree of height h is a binary tree consisting of h + 1 levels. Level 0 consists of a single node called root, level h consists of 2^h nodes called leaves. Each node that is not a leaf has exactly two children, left and right one.

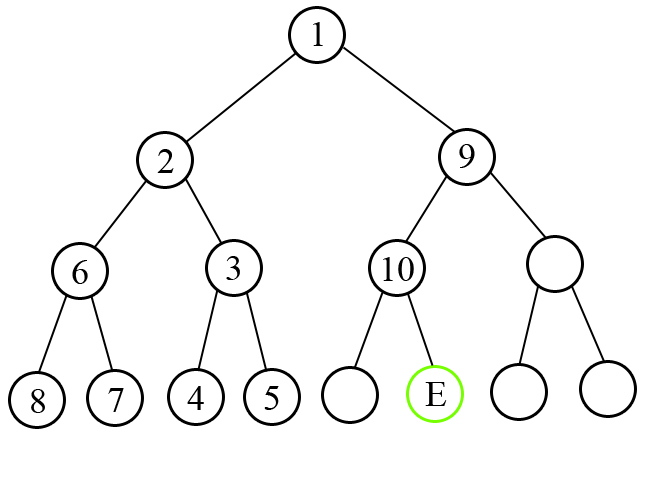
Following picture illustrates the sample test number 3. Nodes are labeled according to the order of visit.

先对整棵数进行考虑

1.如果目标点位于右子树且当前方向向左,则左子树中所有节点和根都必须先访问,然后再考虑右子树,即数量为2^(n+1)-2^n+v(右子树)

2.如果目标点位于右子树且当前方向向右,则根必须先访问,然后再考虑右子树,即数量为1+v(右子树)

3.如果目标点位于左子树且当前方向向右,则右子树中所有节点和根都必须先访问,然后再考虑左子树,即数量为2^(n+1)-2^n+v(左子树)

4.如果目标点位于左子树且当前方向向左,则根必须先访问,然后再考虑左子树,即数量为1+v(左子树)

求子树的节点数和求原树的节点数问题性质相同,故可以递归求解.

#include <iostream>
long long pow(int x)
{
    long long res=1;
    for(int i=1;i<=x;i++)
        res*=2;
    return res;
}

using namespace std;
long long dfs(long long n,long long m,int dir)
{
    if(n==0)
        return 0;
    if(m>pow(n-1))//位于右子树
    {
        if(dir==0)//方向向左
            return pow(n+1)-pow(n)+dfs(n-1,m-pow(n-1),0);
        else//方向向右
            return 1+dfs(n-1,m-pow(n-1),0);
    }
    else//位于左子树
    {
        if(dir==0)//方向向左
            return 1+dfs(n-1,m,1);
        else//方向向右
            return pow(n+1)-pow(n)+dfs(n-1,m,1);
    }
}
int main()
{
    long long n,m;
    cin>>n>>m;
    cout<<dfs(n,m,0)<<endl;
    return 0;
}