noip 模拟赛
先附上T1
不怕噩梦
蚊子最近经常做噩梦,然后就会被吓醒。这可不好。。疯子一直在发愁,然后突然有一天,他发现蚊子其实就是害怕某些事。如果那些事出现在她的梦里,就会害怕。我们可以假定那个害怕的事其实是一个字符串。而她做的梦其实也是一个字符串。
她可以一个晚上一直做梦,所以梦这个字符串会很长,如果其中包含了她所害怕的事情,那么她这天晚上就会害怕。当然一个害怕的事也可能在这天晚上被她梦到很多遍,当然每个晚上也可能有很多种害怕的事都被梦到。
每个害怕的事都有一定的权值。而这天晚上如果梦到了某件事,那么这件事所产生的黑暗效果等于这件 事的权值乘以这个害怕的事在梦字符串里的开始位置。如果同样的事梦到了很多遍,那么就重复上面的操作很多遍。当天晚上的黑暗效果总和等于当天所有害怕的事产生的黑暗效果累加到一起。现在疯子想知道蚊子这些天来噩梦的黑暗效果总和是多少。
INPUT (dream.in):
第1行两个整数N,M代表一共有N天梦和M个害怕的事。
第2行到第M+1行。每行一个字符串ti,代表第I个害怕的事
第M+2行到第2M+2行。每行一个整数ai.代表第I个害怕的事权值
第2M+3行到第N+2M+3行。每行一个字符串si,代表第I天的梦。
OUTPUT(dream.out)
SUM
SUM=N天里黑暗效果的总和。
我们保证每天的黑暗效果都小于maxlongint;
输入样例
2 2
abc
def
1
2
abcdef
defabc
输出样例
15
友情提示:
1*1+2*4+1*4+2*1=15
对于数据的把握和时间复杂度的估计是成败的关键。
如果出现一个梦是:ab
而害怕的事有a,b,ab,那么a,b,ab都需要参与计算..
对于30%的数据
N,M<=50
对于所有的数据
N<=200.M<=200. length(si)<=200.length(ti)<=200.ai<=10.
此题数据级水
模拟一下就好了
我写了一个将近n^4暴力,居然过了?
放上我的代码
1 #include <cstdio> 2 #include <cstdlib> 3 #include <iostream> 4 #include <cstring> 5 #include <algorithm> 6 #include <cmath> 7 using namespace std; 8 const int N=205; 9 char ch1[N][N],ch2[N][N]; 10 int n,m,d[N],len1[N],len2[N],ans; 11 int main() 12 { 13 scanf("%d %d",&n,&m); 14 for(int i=1;i<=m;i++) 15 { 16 scanf("%s",ch1[i]+1); 17 len1[i]=strlen(ch1[i]+1); 18 } 19 for(int i=1;i<=m;i++) 20 scanf("%d",&d[i]); 21 for(int i=1;i<=n;i++) 22 { 23 scanf("%s",ch2[i]+1); 24 len2[i]=strlen(ch2[i]+1); 25 } 26 for(int i=1;i<=m;i++) 27 { 28 for(int j=1;j<=n;j++) 29 { 30 if(len1[i]>len2[j]) 31 continue; 32 for(int k=1;k<=len2[j];k++) 33 { 34 bool flag=true; 35 if(k+len1[i]-1>len2[j]) 36 flag=false; 37 else 38 { 39 for(int pos=k,h=1;h<=len1[i];h++) 40 { 41 if(ch1[i][h]==ch2[j][pos]) 42 { 43 flag=true; 44 } 45 else 46 { 47 flag=false; 48 break; 49 } 50 pos++; 51 } 52 } 53 if(flag) 54 ans+=k*d[i]; 55 } 56 } 57 } 58 printf("%d\n",ans); 59 return 0; 60 }
接下来放上KMP的代码
1 #include<cstdio> 2 #include<cstdlib> 3 #include<iostream> 4 #include<algorithm> 5 #include<cstring> 6 using namespace std; 7 typedef long long ll; 8 char ch[300][300],t[300][300],pre[300]; 9 int d[300]; 10 ll ans=0; 11 inline void check(int a,int b,int len,int len2) 12 { 13 int j=0; 14 for(int i=0;i<=len;i++) 15 { 16 while(j>0&&ch[a][j+1]!=t[b][i+1]) 17 j=pre[j]; 18 if(ch[a][j+1]==t[b][i+1]) 19 j++; 20 if(j==len2) 21 { 22 ans+=d[a]*(i-len2+2); 23 j=pre[j]; 24 } 25 } 26 } 27 inline void calc(int s,int len) 28 { 29 memset(pre,0,sizeof pre); 30 int j=0; pre[1]=0; 31 for(int i=1;i<len;i++) 32 { 33 while(j>0&&ch[s][i+1]!=ch[s][j+1]) 34 j=pre[j]; 35 if(ch[s][i+1]==ch[s][j+1]) 36 j++; 37 pre[i+1]=j; 38 } 39 } 40 int main() 41 { 42 int n,m; 43 scanf("%d %d",&n,&m); 44 for(int i=1;i<=m;i++) 45 scanf("%s",ch[i]+1); 46 for(int i=1;i<=m;i++) 47 scanf("%d",&d[i]); 48 for(int i=1;i<=n;i++) 49 scanf("%s",t[i]+1); 50 for(int i=1;i<=m;i++) 51 { 52 int len=strlen(ch[i]+1),len2; 53 calc(i,len); 54 len2=len; 55 for(int j=1;j<=n;j++) 56 len=strlen(t[j]+1),check(i,j,len,len2); 57 } 58 printf("%lld",ans); 59 return 0; 60 }
T2
那23个路口
故事的起源不加赘述,那23个路口。
单刀直入,我直接说题的意思。
蚊子和疯子在做一件事,就是他们要在茫茫的大街上找一个出发点,然后从出发点开始,经过上下左右23次拐弯,到达一个他们也不知道的地方。
老城的街道排列的十分有规律,于是疯子和蚊子把老城的街道排布画在了一张地图上。地图上每一个点代表一个地方,而这个地方有一定的憧憬值,疯子希望可以带蚊子走过的二十三个路口的憧憬值总和是所有方案中最大的。
现在我们读入一个矩阵,如果此点为0,则这个点为起点,如果此点为-1,则这个点为障碍点,否则这个数代表憧憬值。注意起点和障碍点是没有憧憬值的,起点只有开始的时候可以达到,不可以再回来。而障碍点根本就不可以走过。这样一来,请你选择合适的路线,使走完23个路口后得到最大的憧憬值,有憧憬值的点可以重复进出,每次可以选择四个方向,上下左右。起点为第0个路口
输入格式:
第1行两个整数 n,m (茫茫大街的长和宽)
第2行到第m+1行,每行n个整数 Aij(第I行第j个地点的憧憬值)
输出格式
一个整数sum (可以得到的最大憧憬值)
INPUT
4 4
1 1 1 1
1 1 0 1
1 1 1 1
1 1 1 1
OUTPUT
23
对于30%的数据,n,m<=50
对于全部数据 n,m<=300
0<n,m<300,每个点的憧憬值可以用longint表示。
不知道为什么,数据都非常水
我看到了300*300的范围,果断放弃了dfs
于是我开始想dp怎么写
其实dp方程非常简单
dp[i][j][k]表示,当前走到了i,j这个坐标,走了k步,所能获得的最大值
转移方程就只有4个
dp[i][j][k]=max(dp[i][j][k],dp[i-1][j][k-1]+d[i][j]);
dp[i][j][k]=max(dp[i][j][k],dp[i+1][j][k-1]+d[i][j]);
dp[i][j][k]=max(dp[i][j][k],dp[i][j-1][k-1]+d[i][j]);
dp[i][j][k]=max(dp[i][j][k],dp[i][j+1][k-1]+d[i][j]);
是不是很简单
但是此题有坑!!!!!!
题目中的n是列数,m是行数
所以我痛失100分
放上我的代码
1 #include <cstdio> 2 #include <cstdlib> 3 #include <iostream> 4 #include <algorithm> 5 #include <cstring> 6 #include <cmath> 7 using namespace std; 8 typedef long long ll; 9 const int N=305; 10 ll dp[N][N][25],d[N][N],n,m,ans=-999999999999; 11 int main() 12 { 13 memset(dp,-0x3f,sizeof(dp)); 14 scanf("%lld %lld",&n,&m); 15 memset(d,-1,sizeof(d)); 16 for(ll i=1;i<=n;i++) 17 for(ll j=1;j<=m;j++) 18 { 19 scanf("%lld",&d[i][j]); 20 if(d[i][j]==0) 21 dp[i][j][0]=0; 22 } 23 24 for(ll k=1;k<=23;k++) 25 for(ll i=1;i<=n;i++) 26 for(ll j=1;j<=m;j++) 27 { 28 if(d[i][j]!=-1) 29 { 30 if(d[i-1][j]!=-1) 31 dp[i][j][k]=max(dp[i][j][k],dp[i-1][j][k-1]+d[i][j]); 32 if(d[i+1][j]!=-1) 33 dp[i][j][k]=max(dp[i][j][k],dp[i+1][j][k-1]+d[i][j]); 34 if(d[i][j-1]!=-1) 35 dp[i][j][k]=max(dp[i][j][k],dp[i][j-1][k-1]+d[i][j]); 36 if(d[i][j+1]!=-1) 37 dp[i][j][k]=max(dp[i][j][k],dp[i][j+1][k-1]+d[i][j]); 38 } 39 } 40 for(ll i=1;i<=n;i++) 41 for(ll j=1;j<=m;j++) 42 { 43 ans=max(ans,dp[i][j][23]); 44 } 45 printf("%lld\n",ans); 46 return 0; 47 }
T3
我们的可可西里
转眼到了2008年的6月9日,盼望已久的高考结束了。我们踏上了向西的旅程(本来是想写西去之路,可是考虑不太妥当)。可可西里,多么诱人的名词,充满了奇幻的色彩和自然的淳朴。从可可西里徒步走回家的决定是在1年半前定下的,而现在,终于可以实现那个钩过手指的预定。我们的可可西里。。。
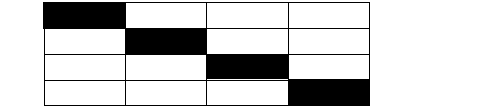
在回家的路上,疯子和蚊子看到了许多可爱的藏羚羊,无意之中疯子和蚊子发现藏羚羊的居住地的分布也是有规律的,虽然疯子和蚊子早就听说藏羚羊是一种群体性很强又有超高IQ的动物,但是还是为它们的居住地分布规律感到惊叹。经过细心的观察,疯子和蚊子发现,如果假设一个藏羚羊群体有N只羊,就可以把它们的领地当做一个N*N的方阵,在这个方阵上第I列的第I 行都有一个圣地,它们不会居住在圣地,同时每行每列只能居住一只羚羊。于是他们很快算出一个有N只羊的藏羚羊群体的居住地分布方法数。
这是圣地的一种排列方法
INPUT:
一个整数N 代表藏羚羊的个数
OUTPUT:
一个整数sum代表方法数
输入样例:
4
输出样例:
9
对于30%的数据,n<=10
对于全部数据 n<=1000
下面是标准题解:
错排问题。
瑞士数学家欧拉推出个公式
f(n)=n!(1/2!-1/3!+1/4!+..+(-1)^n/n!)
我不是瑞士数学家。所以我给大家一个递推公式。
First
易得 f[1]:=0;f[2]:=1;
Second
假设我们已经得到 f[k-2],f[k-1].现在想求 f[k].
1.K 可以与从 1 在 K -1 中任意一个棋子 I 交换,这样固定了 2 个棋子,剩下 K-2
棋子的排列方法数为 f[K-2].那么按照这种 K 和 1 到 K-1 中交换棋子可以得到的方案总数
为(K-1)*f[K-2];
2.K 可以放在 1 到 K-1 中的任何一个位置 I,并且 I 不放到 K 个位置上,其实这样
就等效于 f[K-1]种方法,所以这种策略的总和为(K-1)*f[K-1].
所以我们便得到了个递推公式 f[K]:=(K-1)*(f[K-1]+f[K-2]);
当然数据范围需要应用到高精度。
然后用题目中的公式带进去就可以了
高精度不要打错了
1 #include<cstdio> 2 #include<cstdlib> 3 #include<iostream> 4 #include<algorithm> 5 #include<cstring> 6 using namespace std; 7 int a[10000],b[10000],c[10000],d[100],e[10000]; 8 inline void add() { 9 int maxn=max(a[0],b[0]); 10 for(int i=1;i<=maxn;i++) 11 { 12 c[++c[0]]+=a[i]+b[i]; 13 if(c[c[0]]>=10) 14 c[c[0]+1]+=c[c[0]]/10; 15 c[c[0]]%=10; 16 } 17 if(c[c[0]+1]) 18 c[0]++; 19 } 20 inline void mul(int k) 21 { 22 while(k) 23 { 24 d[++d[0]]=k%10; 25 k/=10; 26 } 27 for(int i=1;i<=c[0];i++) 28 for(int j=1;j<=d[0];j++) 29 { 30 e[i+j-1]+=c[i]*d[j]; 31 if(e[i+j-1]>=10) 32 e[i+j]+=e[i+j-1]/10,e[i+j-1]%=10; 33 } 34 int pos=c[0]+d[0]; 35 while(!e[pos] && pos>=2) 36 pos--; 37 e[0]=pos; 38 } 39 inline void change(int k) { 40 add(); 41 mul(k); 42 memset(a,0,sizeof a); 43 memcpy(a,b,sizeof(int)*(b[0]+1)); 44 memset(b,0,sizeof b); 45 memcpy(b,e,sizeof(int)*(e[0]+1)); 46 memset(c,0,sizeof c); 47 memset(d,0,sizeof d); 48 memset(e,0,sizeof e); 49 } 50 int main() { 51 int n; 52 scanf("%d",&n); 53 a[++a[0]]=0; 54 b[++b[0]]=1; 55 for(int i=3;i<=n;i++) 56 { 57 change(i-1); 58 } 59 for(int i=b[0];i;i--) 60 printf("%d",b[i]); 61 return 0; 62 }
T4
我们的公司
长大了。
疯子和蚊子有了自己的公司。为了活跃公司内部的气氛,使员工时刻保持开心的状态,疯子和蚊子照例举办了一年一度的五子棋大赛。蚊子和疯子都是超超一流的好手,于是总是在决赛中碰面,可是总是疯子第二,蚊子第一,疯子不服气,于是乎,疯子想出了个新的五子棋玩法想得到了冠军,就是在一个n*m的棋盘中,去掉若干个棋子,使这个棋盘里不存在任何五子棋连线(也就是没有五个连续的棋子横行,纵行,斜行),他们要比的就是谁去掉最少的棋子可以实现要求。你能猜出疯子是怎么赢的么。
例如当n=5 m=5 的时候
|
|
棋子 |
棋子 |
棋子 |
棋子 |
|
棋子 |
|
棋子 |
棋子 |
棋子 |
|
棋子 |
棋子 |
|
棋子 |
棋子 |
|
棋子 |
棋子 |
棋子 |
|
棋子 |
|
棋子 |
棋子 |
棋子 |
棋子 |
|
如图,只需要去掉5个棋子就可以完成题目的要求,而且易证不可能有比去掉比5个棋子更小的方案。
INPUT:
一行两个整数n,m表示棋盘的长和宽
OUTPUT
一行一个整数k表示最少去掉的棋子数。
输入样例:
5 5
输出样例
5
n,m<=10
这也是一道找规律
你多带几组数进去算一下
就可以发现一个神奇的规律
ans=n*m/5
然后就a了
1 #include <cstdio> 2 #include <cstdlib> 3 using namespace std; 4 int main() 5 { 6 int n,m; 7 scanf("%d %d",&n,&m); 8 if(n<=4 && m<=4) 9 printf("0\n"); 10 else 11 printf("%d\n",n*m/5); 12 return 0; 13 }
这题也可以用bfs,像是马走日的方式bfs
我同学写的,他们推出的规律,也能过掉
1 #include <bits/stdc++.h> 2 using namespace std; 3 int py[4][2]={{2,-1},{1,2},{-1,-2},{-2,1}}; 4 int n,m,num,ans=9999999; 5 bool vis[20][20]; 6 struct node 7 { 8 int x,y; 9 node(int xx,int yy) 10 { 11 x=xx,y=yy; 12 } 13 }; 14 queue <node>q; 15 int main() 16 { 17 scanf("%d%d",&n,&m); 18 for(int i=1;i<=n;i++) 19 for(int j=1;j<=m;j++) 20 { 21 if(vis[i][j]) 22 continue; 23 num=0; 24 q.push(node(i,j)); 25 while(!q.empty()) 26 { 27 node p=q.front(); 28 q.pop(); 29 for(int k=0;k<4;k++) 30 { 31 int x=p.x+py[k][0]; 32 int y=p.y+py[k][1]; 33 if(x<1 || x>n || y<1 || y>m) 34 continue; 35 if(!vis[x][y]) 36 { 37 vis[x][y]=1; 38 q.push(node(x,y)); 39 num++; 40 } 41 } 42 } 43 ans=min(ans,num); 44 } 45 printf("%d",ans); 46 return 0; 47 }
我这个蒟蒻只拿了220分
本来可以300的
下次应注意


