洛谷 1273 有线电视网
我一直觉得这题的题解写的有问题
大多数题解都说他是分组背包
但是我觉得这并不是分组背包,与分组背包有差别
咱们先看看题

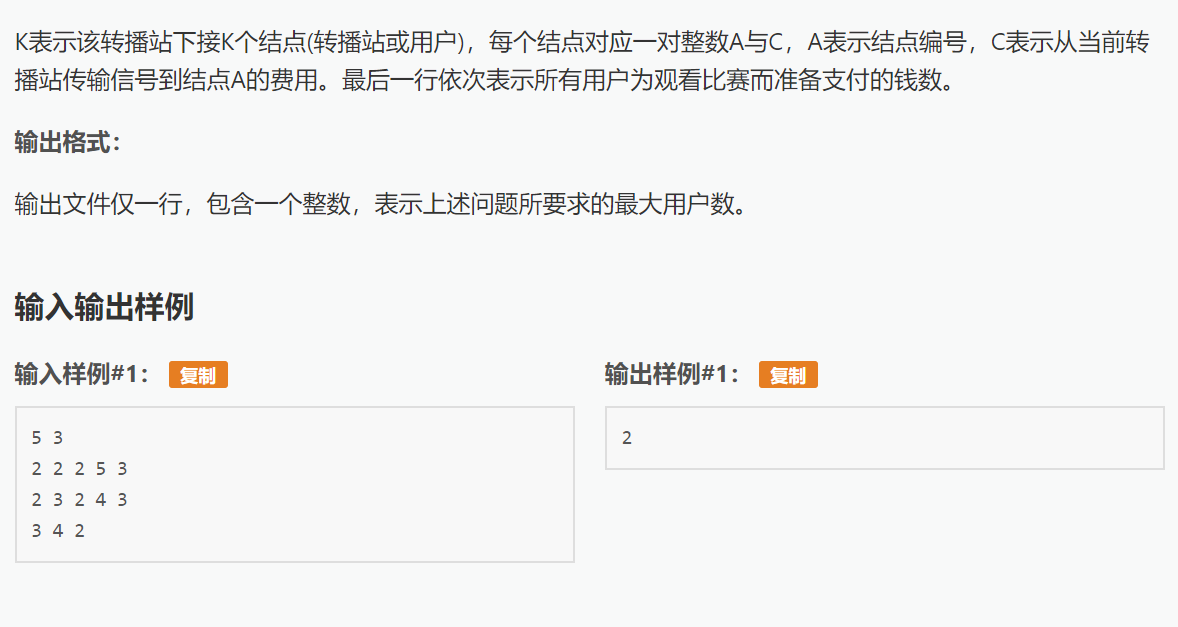

题意就是要在不亏本的情况下,使最多的叶子节点看到比赛
咱们来想想这题的思路
这是典型的树形dp
也是我做的第一道树形dp
我们考虑一下dp方程
我们设dp[i][j],表示以i为根节点,满足j个客户所能获得的最大值
如何转移?
dp[i][j]=max(dp[i][j-k]+dp[x][k],dp[i][j]) x为i的儿子节点
在dfs时就可以计算出每个节的孩子数
看看代码,有注释
1 #include <cstdio> 2 #include <cstdlib> 3 #include <iostream> 4 #include <algorithm> 5 #include <vector> 6 #include <cstring> 7 using namespace std; 8 const int N=3005; 9 struct node 10 { 11 int x,v; 12 node(int xx,int vv) 13 { 14 x=xx,v=vv; 15 } 16 }; 17 vector <node> g[N]; 18 int n,m,k,x,y,d[N],dp[N][N]; 19 int dfs(int x) 20 { 21 if(x>n-m) 22 { 23 dp[x][1]=d[x];//到根节点这个点的值肯定为他自身的值 24 return 1; 25 } 26 int sum=0,t; 27 for(int i=0;i<g[x].size();i++) 28 { 29 t=dfs(g[x][i].x); 30 sum+=t;//sum为他的总孩子节点个数 31 for(int j=sum;j>0;j--) 32 { 33 for(int kk=1;kk<=t;kk++)//t为他的孩子的孩子节点个数 34 { 35 if(j-kk>=0) 36 dp[x][j]=max(dp[x][j],dp[x][j-kk]+dp[g[x][i].x][kk]-g[x][i].v);//dp过程 37 } 38 } 39 } 40 return sum; 41 } 42 int main() 43 { 44 scanf("%d %d",&n,&m); 45 int v=n-m; 46 for(int i=1;i<=v;i++) 47 { 48 scanf("%d",&k); 49 for(int j=1;j<=k;j++) 50 { 51 scanf("%d %d",&x,&y); 52 g[i].push_back(node(x,y));//加边 53 } 54 } 55 for(int i=n-m+1;i<=n;i++) 56 scanf("%d",&d[i]); 57 memset(dp,~0x3f,sizeof(dp)); 58 for(int i=1;i<=n;i++) 59 dp[i][0]=0;//初始化,每个节点选0个孩子肯定是0 60 dfs(1); 61 for(int i=m;i>=1;i--) 62 { 63 if(dp[1][i]>=0)//大于零就可以选 64 { 65 printf("%d\n",i); 66 break; 67 } 68 } 69 return 0; 70 }
这题就解决了


