洛谷 1282 多米诺骨牌

说实话这一题我没想出来，果然是我太蒻了

后来看了看题解才发现，原来这就是一个01背包，其实之前也有往这方面去想，但是没想出来。

不说废话了，咱们看看题目

 

题目描述

多米诺骨牌有上下2个方块组成，每个方块中有1~6个点。现有排成行的

上方块中点数之和记为S1，下方块中点数之和记为S2，它们的差为|S1-S2|。例如在图8-1中，S1=6+1+1+1=9，S2=1+5+3+2=11，|S1-S2|=2。每个多米诺骨牌可以旋转180°，使得上下两个方块互换位置。 编程用最少的旋转次数使多米诺骨牌上下2行点数之差达到最小。

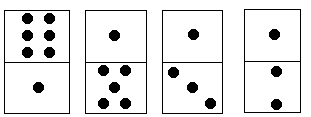
对于图中的例子，只要将最后一个多米诺骨牌旋转180°，可使上下2行点数之差为0。

输入输出格式

输入格式：

 

输入文件的第一行是一个正整数n(1≤n≤1000)，表示多米诺骨牌数。接下来的n行表示n个多米诺骨牌的点数。每行有两个用空格隔开的正整数，表示多米诺骨牌上下方块中的点数a和b，且1≤a，b≤6。

 

输出格式：

 

输出文件仅一行，包含一个整数。表示求得的最小旋转次数。

 

题目的意思已经很明确了，咋们来看看做法

首先，每个多米诺骨牌只有两种选法，转或者不转

emmm，这不就是01背包吗？

但是01背包他有一定的容积，怎么往这个方面去想呢？

我们可以从小到大枚举每一个差值，如果可以到达这种差值，则一定是最优解了

但是他会出现负数怎么办，我一开始就想到了，加上一个稍微大一点的数就可以了

dp方程就写出来了

 

dp[j]=min(INF,dp[j-a[i]],dp[j-b[i]]+1)

 

代码实现如下

#include <cstdio>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N=1005;
const int INF=999999999;
int a[N],b[N],dp[N*6],sum,maxn,n;
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d %d",&a[i],&b[i]);
        maxn+=max(a[i],b[i]);
        sum+=a[i]+b[i];
    }
    memset(dp,0x3f,sizeof(dp));//初始化为正无穷
    dp[0]=0;//边界
    for(int i=1;i<=n;i++)
        for(int j=maxn;j>=0;j--)
        {
            int temp=INF;//假设到达不了
            if(j>=a[i])
                temp=dp[j-a[i]];
            if(j>=b[i])
                temp=min(temp,dp[j-b[i]]+1);
            dp[j]=temp;//强制选或不选
        }//01背包的过程
    int k;
    for(int i=sum>>1;i;i--)
    {
        k=min(dp[i],dp[sum-i]);//对称的
        if(k<INF)
        {
            printf("%d\n",k);
            return 0;
        }
    }
    return 0;
}

这题还是要好好看看的

也许有些大佬觉得这题很水