LCA最近公共祖先
1.ST表+时间戳
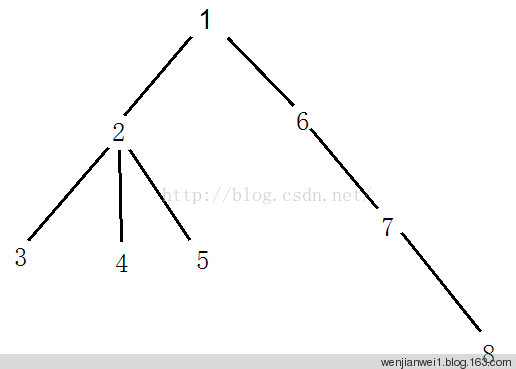
DFS记录这棵树每个点出现的时间1 2 3 2 4 2 5 2 1 6 7 8 7 6 1。
然后用ST表记录每个区间的min值，然后进行q次查询，时间复杂度O(Nlog2N+Qlog2N);
#include<iostream>
#include<stdio.h>
#include<stdlib.h>
#include <iomanip>
#include<cmath>
#include<float.h>
#include<string.h>
#include<algorithm>
#define sf scanf
#define scf(x) scanf("%d",&x)
#define scff(x,y) scanf("%d%d",&x,&y)
#define pf printf
#define prf(x) printf("%d\n",x)
#define mm(x,b) memset((x),(b),sizeof(x))
#include<vector>
#include<queue>
#include<map>
#define rep(i,a,n) for (int i=a;i<n;i++)
#define per(i,a,n) for (int i=a;i>=n;i--)
typedef long long ll;
const ll mod=1e9+100;
const double eps=1e-8;
using namespace std;
const double pi=acos(-1.0);
const int inf=0xfffffff;
const int N = 1010;
int rmq[2*N];//rmq数组，就是欧拉序列对应的深度序列
struct ST
{
int mm[2*N];
int dp[2*N][20];//最小值对应的下标
void init(int n)
{
mm[0] = -1;
for(int i = 1;i <= n;i++)
{
mm[i] = ((i&(i-1)) == 0)?mm[i-1]+1:mm[i-1];
dp[i][0] = i;
}
for(int j = 1; j <= mm[n];j++)
for(int i = 1; i + (1<<j) - 1 <= n; i++)
dp[i][j] = rmq[dp[i][j-1]] < rmq[dp[i+(1<<(j-1))][j-1]]?dp[i][j-1]:dp[i+(1<<(j-1))][j-1];
}
int query(int a,int b)//查询[a,b]之间最小值的下标
{
if(a > b) swap(a,b);
int k = mm[b-a+1];
return rmq[dp[a][k]] <= rmq[dp[b-(1<<k)+1][k]]?dp[a][k]:dp[b-(1<<k)+1][k];
}
};
//边的结构体定义
struct Edge
{
int to,next;
};
Edge edge[N*2];
int tot,head[N];
int F[N*2];//欧拉序列，就是dfs遍历的顺序，长度为2*n-1,下标从1开始
int P[N];//P[i]表示点i在F中第一次出现的位置
int cnt;
ST st;
void init()
{
tot = 0;
memset(head,-1,sizeof(head));
}
void addedge(int u,int v)//加边，无向边需要加两次
{
edge[tot].to = v;
edge[tot].next = head[u];
head[u] = tot++;
}
void dfs(int u,int pre,int dep)
{
F[++cnt] = u;
rmq[cnt] = dep;
P[u] = cnt;
for(int i = head[u];i != -1;i = edge[i].next)
{
int v = edge[i].to;
if(v == pre)continue;
dfs(v,u,dep+1);
F[++cnt] = u;
rmq[cnt] = dep;
}
}
void LCA_init(int root,int node_num)//查询LCA前的初始化
{
cnt = 0;
dfs(root,root,0);
st.init(2*node_num-1);
}
int query_lca(int u,int v)//查询u,v的lca编号
{
return F[st.query(P[u],P[v])];
}
bool root[N];
int main()
{
int n,m,num,v,u;
while(~scff(n,m))//n个点，m个查询点
{
init();
mm(root,true);
rep(i,1,n)
{
sf("%d %d",&u,&v);
addedge(u,v);
addedge(v,u);
root[v]=false;
}
int temp;
rep(i,1,n+1)
{
if(root[i])
{
temp=i;break;
}
}
LCA_init(temp,n);
while(m--)
{
scanf("%d%d",&u,&v);
prf(query_lca(u,v));
}
}
return 0;
}
2.targin
targin的多个查询的话还不会，似乎也可以的，后面学学要怎么做
const int N=1e4+3;
int node[N];
bool root[N];
int cnt;
int visit[N];
int fa[N];
int le,ri;
struct Edge
{
int v,next;
}edge[N];
void add_edge(int u,int v)
{
edge[cnt].next=node[u];
edge[cnt].v=v;
node[u]=cnt++;
}
int find(int x)
{
if(fa[x]==x) return x;
return fa[x]=find(fa[x]);
}
void Union(int x,int y)
{
x=find(x);
y=find(y);
if(x!=y)
fa[y]=x;
}
void tarjin(int x)
{
for(int i=node[x];i!=-1;i=edge[i].next)
{
tarjin(edge[i].v);
Union(x,edge[i].v);
}
visit[x]=1;
if(x==le&&visit[ri])
{
prf(find(ri));
return ;
}
if(x==ri&&visit[le])
{
prf(find(le));
return ;
}
}
int main()
{
int re,x,y;
scf(re);
while(re--)
{
mm(fa,-1);
mm(root,true);
mm(node,-1);
mm(visit,0);
int n;
cnt=0;
scf(n);
rep(i,1,n)
{
scff(x,y);
root[y]=false;
fa[i]=i;
add_edge(x,y);
}
fa[n]=n;
scff(le,ri);
rep(i,1,n+1)
if(root[i])
{
tarjin(i);
break;
}
}
return 0;
}
