凸包问题

扫描法：O(n*lgn)

先取一点最下，最左的点开始，以它为基点，做极坐标方程，其他点按角度排序，角度相同按对它的距离排序；
后面以下一个点为基点排序，但是如果在用sort，复杂度就变成O(n^2)了，所以不能这样；（衍生出一种题目，如果数据不多，而且要求以蚊香式输出点的话可以这样）
所以对下一点为基点，用direction的方法求下面的点对这个基点的极坐标排，也就是在模板最后面的while里面，如果下下个的角度大于或者等于下一个，那么下下个就要覆盖下一个，也就是top--；然后绕完一圈就可以了；
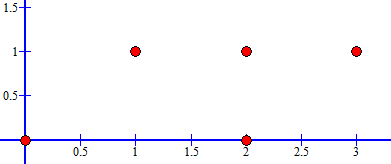
图示

注意这样的只能取到除(2，1)的四个点

叉积 平面向量很好计算
例如： a=（x1,y1）,b=(x2,y2)
则 a×b=x1y2-x2y1;
叉积的运用：
a×b>0 则说明 b在a的左上方
a×b<0 则说明b在a的右下方
模板

const int INF=0xfffffff ;
struct Point{
    int x,y,temp;
}p[50005],s[50005];
int top;
int direction(Point p1,Point p2,Point p3) { return (p3.x-p1.x)*(p2.y-p1.y)-(p2.x-p1.x)*(p3.y-p1.y); }//从1到2的向量和从1到3的向量，如果到3的向量在到2的右边，就是大于0的
double dis(Point p1,Point p2) { return sqrt((p2.x-p1.x)*(p2.x-p1.x)+(p2.y-p1.y)*(p2.y-p1.y)); }
bool cmp(Point p1,Point p2)//极角排序 
{
    int temp=direction(p[0],p1,p2);
    if(temp<0)return true ;
    if(temp==0&&dis(p[0],p1)<dis(p[0],p2))return true;
	return false;
}
void Graham(int n)
{
    int pos,minx,miny;
    minx=miny=INF;
    for(int i=0;i<n;i++)//找最下面的基点
        if(p[i].y<miny||(p[i].y==miny&&p[i].x<minx))
        {
            minx=p[i].x;
            miny=p[i].y;
            pos=i;
        }
    swap(p[0],p[pos]);
    sort(p+1,p+n,cmp);
    p[n]=p[0];
    s[0]=p[0];s[1]=p[1];s[2]=p[2];
    top=2;
    for(int i=3;i<=n;i++)
    {
        while(direction(s[top-1],s[top],p[i])>=0&&top>=2)top--;//所以在右边的话，就要退回去覆盖
        s[++top]=p[i] ;
    }
}

符合退回去的图

int direction(Point p1,Point p2,Point p3) { return (p3.x-p1.x)(p2.y-p1.y)-(p2.x-p1.x)(p3.y-p1.y); }//从1到2的向量和从1到3的向量，如果到3的向量在到2的右边，就是大于0的
这个代码，还可以表示p1点与直线p2.p3的关系，direction>0表示在直线左边