Attention的计算过程
本文参考以及图片来源Transformer详解
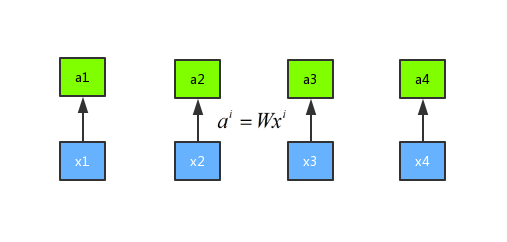
首先假设我们有序列 x1、x2、x3 和 x4 这四个序列,首先我们进行一次权重的乘法 \({a^i} = W{x^i}\) ,得到新的序列 a1、a2、a3 和 a4。示意图如下所示:
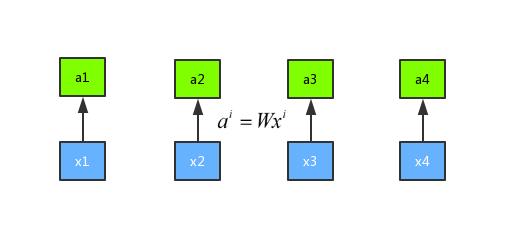
然后我们将输入 a 分别乘以三个不同的权重矩阵 W 分别得到 q、k、 v 三个向量,公式分别是\({q^i} = {W^q}{a^i}\)、${k^i} = {W^k} {v^i} \(、\)v^i = {Wv}{ai}$,这里面 q 表示的是 query,是需要 match 其他的向量的;k 表示的是 key,是需要被 q 来match的,v 表示 value,表示需要被抽取出来的信息。示意图如下所示:
接下来我们需要做的就是将每一个query q 对每一个key k 做 attention 操作,那么 attention 操作是如何做呢,目的是输入两个向量,输出一个数,那么我们可以将这两个向量做内积:q1 和 k1 做attention 得到\(\alpha_{1,1}\) ,q1 和 k2 做attention 得到 \(\alpha_{1,2}\),q1 和 k3 做attention 得到 \(\alpha_{1,3}\),q1 和 k4 做attention 得到\(\alpha_{1,4}\)。其中,attention 的操作可以用很多方法来做,这里我们可以用到一种叫做 scaled 点积,公式是\({\alpha _{1,i}} = q1 \cdot ki/\sqrt d\),这里的 d 表示 q 和 v 的维度。做 attention 的流程如下图所示:
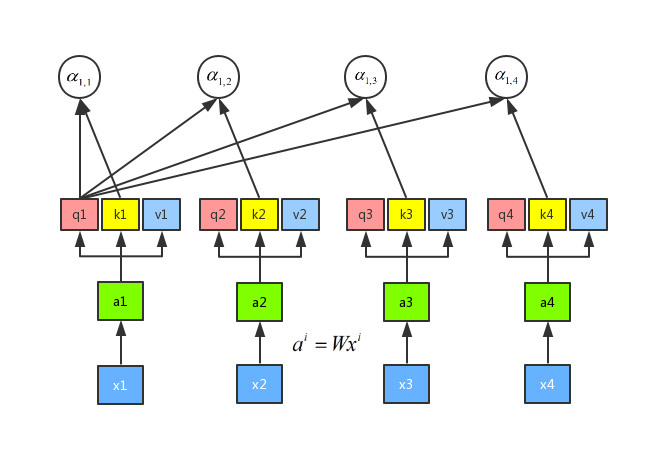
最后我们将\(\alpha _{1,1}\),\(\alpha _{1,2},\),\(\alpha _{1,3}\),\(\alpha _{1,4}\),这四个值进行一个 softmax 操作,得到\({\hat \alpha _{1,1}}\),\({\hat \alpha _{1,2}}\),\({\hat \alpha _{1,3}}\),\({\hat \alpha _{1,4}}\),如图所示:
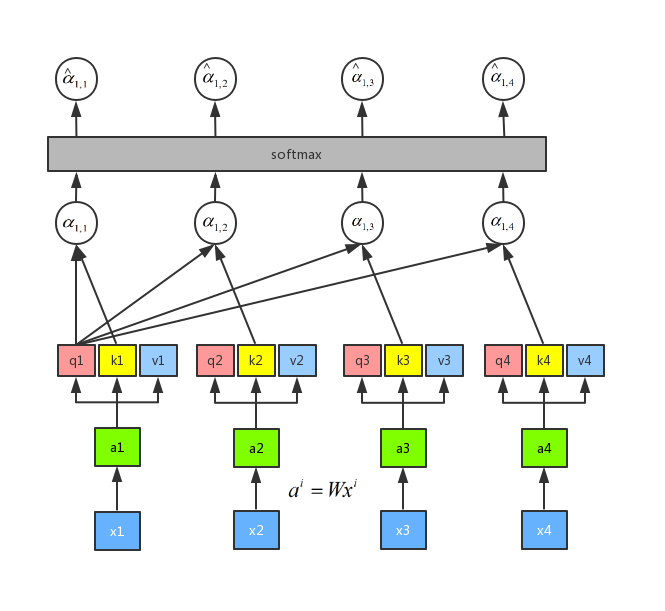
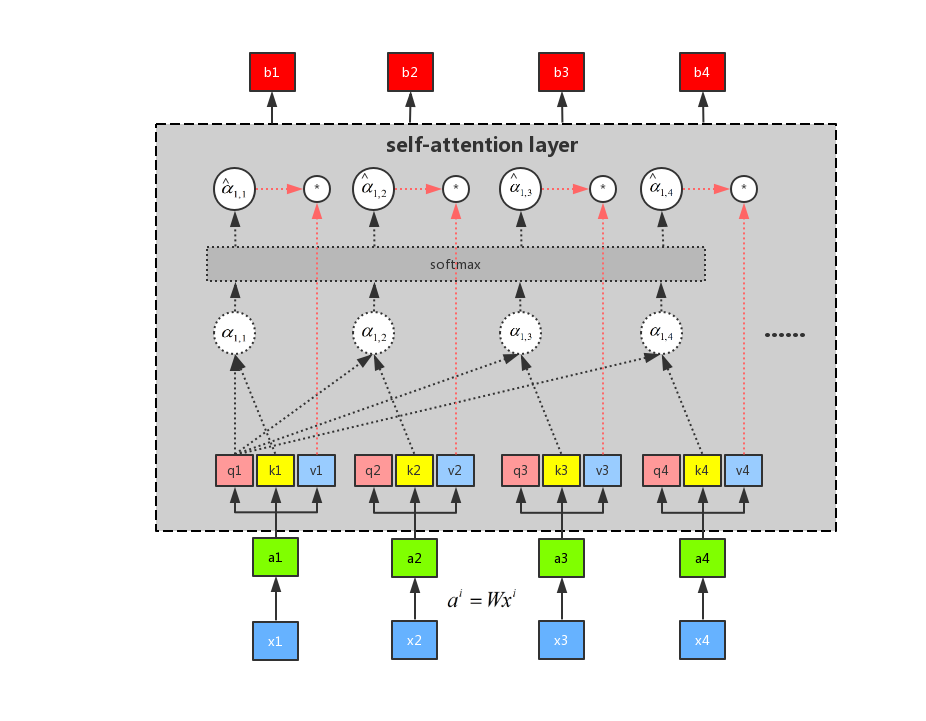
有了 softmax 的输出之后,我们再通过公式\(\sum\limits_i {{{\hat \alpha }_{1,i}} \cdot vi}\) ,将\({{{\hat \alpha }_{1,i}}}\) 分别和\(v_i\)进行点乘之后再求和可以得到 \(b_1\)。整个流程如图所示:
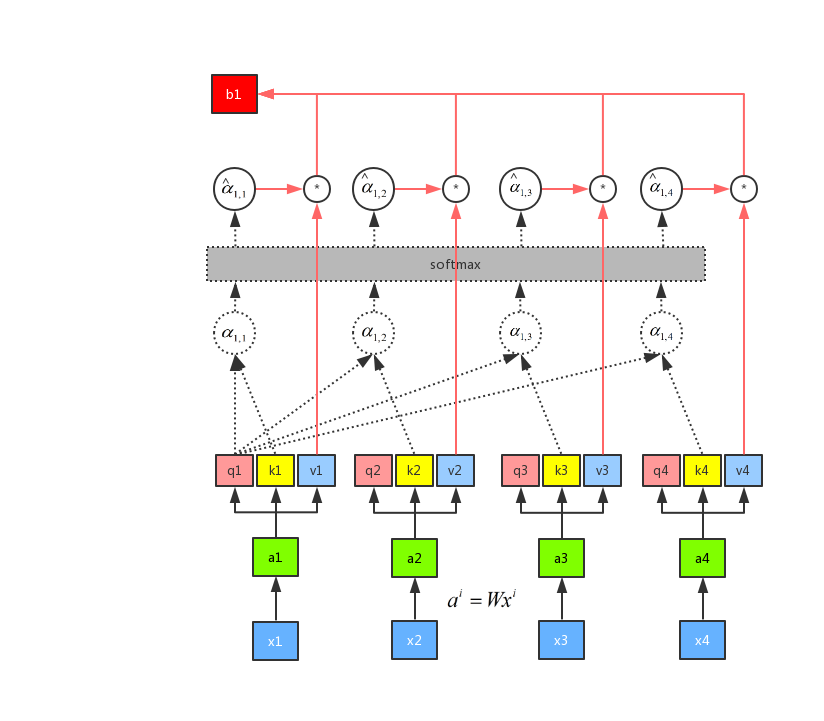
由上图可以知道,我们求得 b1 的时候,已经看到了a2、a3 和 a4 的输入。所以这个时候的输出,有机会浏览到整个序列。但是每一个输出的序列都有自己重点关注的地方,这个就是 attention 机制的精髓所在,我们可以通过控制\({\hat \alpha _{1,1}}\),\({\hat \alpha _{1,2}}\),\({\hat \alpha _{1,3}}\),\({\hat \alpha _{1,4}}\) 来控制我们当前输出所关注的序列权重,如果某一块序列需要被关注,那么就赋予对应\(\alpha\) 值的高权重,反之则相反。这是用 q1 做attention 可以求得 整个的输出 b1,同理我们可以用 q2、q3 和 q4 分别做 attention 求得 b2、b3 和 b4。而且b1、b2、b3 和 b4 是平行被计算出来的,互相是没有先后顺序的影响的。所以整个中间的计算过程可以看做是一个 self-attention layer,输入 x1、x2、x3 和 x4,输出是 b1、b2、b3 和 b4。示意图如图所示: