BZOJ2818: Gcd

Description

给定整数N，求1<=x,y<=N且Gcd(x,y)为素数的
数对(x,y)有多少对.

 

Input

一个整数N

Output

如题

Sample Input

4

Sample Output

4

HINT

 

hint

对于样例(2,2),(2,4),(3,3),(4,2)

1<=N<=10^7

 

手推公式可得

 

 

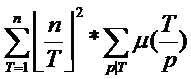
对于每个p更新其倍数，因为[1,n]的素数是O(n/lnn)级别的，而Σn/i是对每个i均摊O(lnn)的，所以总复杂度近似为O(n)。

#include<cstdio>
#include<cctype>
#include<queue>
#include<cmath>
#include<cstring>
#include<algorithm>
#define rep(i,s,t) for(int i=s;i<=t;i++)
#define dwn(i,s,t) for(int i=s;i>=t;i--)
#define ren for(int i=first[x];i;i=next[i])
using namespace std;
const int BufferSize=1<<16;
char buffer[BufferSize],*head,*tail;
inline char Getchar() {
    if(head==tail) {
        int l=fread(buffer,1,BufferSize,stdin);
        tail=(head=buffer)+l;
    }
    return *head++;
}
inline int read() {
    int x=0,f=1;char c=getchar();
    for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
    for(;isdigit(c);c=getchar()) x=x*10+c-'0';
    return x*f;
}
typedef long long ll;
const int maxn=10000010;
int vis[maxn],pri[maxn/10],mu[maxn],f[maxn],cnt;
void solve(int n) {
    vis[1]=mu[1]=1;
    rep(i,2,n) {
        if(!vis[i]) pri[++cnt]=i,mu[i]=-1;
        rep(j,1,cnt) {
            if(i*pri[j]>n) break;
            vis[i*pri[j]]=1;
            if(i%pri[j]==0) {mu[i*pri[j]]=0;break;}
            mu[i*pri[j]]=-mu[i];
        }
    }
    rep(i,1,cnt) {
        int x=pri[i];
        for(int j=x;j<=n;j+=x) f[j]+=mu[j/x];
    }
    ll ans=0;
    rep(i,1,n) ans+=(ll)(n/i)*(n/i)*(ll)f[i];
    printf("%lld\n",ans);
}
int main() {
    solve(read());
    return 0;
}