BZOJ3884: 上帝与集合的正确用法

Description

 

根据一些书上的记载，上帝的一次失败的创世经历是这样的：

第一天， 上帝创造了一个世界的基本元素，称做“元”。

第二天， 上帝创造了一个新的元素，称作“α”。“α”被定义为“元”构成的集合。容易发现，一共有两种不同的“α”。

第三天， 上帝又创造了一个新的元素，称作“β”。“β”被定义为“α”构成的集合。容易发现，一共有四种不同的“β”。

第四天， 上帝创造了新的元素“γ”，“γ”被定义为“β”的集合。显然，一共会有16种不同的“γ”。

如果按照这样下去，上帝创造的第四种元素将会有65536种，第五种元素将会有2^65536种。这将会是一个天文数字。

然而，上帝并没有预料到元素种类数的增长是如此的迅速。他想要让世界的元素丰富起来，因此，日复一日，年复一年，他重复地创造着新的元素……

然而不久，当上帝创造出最后一种元素“θ”时，他发现这世界的元素实在是太多了，以致于世界的容量不足，无法承受。因此在这一天，上帝毁灭了世界。

至今，上帝仍记得那次失败的创世经历，现在他想问问你，他最后一次创造的元素“θ”一共有多少种？

上帝觉得这个数字可能过于巨大而无法表示出来，因此你只需要回答这个数对p取模后的值即可。

你可以认为上帝从“α”到“θ”一共创造了10^9次元素，或10^18次，或者干脆∞次。

 

一句话题意：

 

 

Input

 

接下来T行，每行一个正整数p，代表你需要取模的值

 

Output

T行，每行一个正整数，为答案对p取模后的值

 

Sample Input

3
2
3
6

Sample Output

0
1
4

HINT

 

对于100%的数据，T<=1000,p<=10^7

 

拓展欧拉定理：

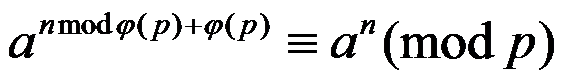
对于任意自然数a,n,p均成立。

设ans=f[p]，则

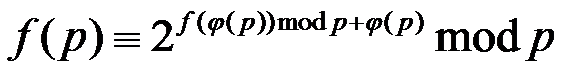
因为对于任意[1,10^7]的整数，它最多进行logn次操作就能变成1，所以暴力求的话就单次O(sqrt(n)logn)了。

#include<cstdio>
#include<cctype>
#include<queue>
#include<cmath>
#include<cstring>
#include<algorithm>
#define rep(i,s,t) for(int i=s;i<=t;i++)
#define dwn(i,s,t) for(int i=s;i>=t;i--)
#define ren for(int i=first[x];i;i=next[i])
using namespace std;
inline int read() {
    int x=0,f=1;char c=getchar();
    for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
    for(;isdigit(c);c=getchar()) x=x*10+c-'0';
    return x*f;
}
typedef long long ll;
int pow(ll n,int m,int p) {
    ll ans=1;
    while(m) m&1?(ans*=n)%=p:1,(n*=n)%=p,m>>=1;
    return (int)ans;
}
int phi(int n) {
    int ans=n;
    for(int i=2;i*i<=n;i++) if(n%i==0) {
        while(n%i==0) n/=i;
        ans=ans/i*(i-1);
    }
    if(n>1) ans=ans/n*(n-1);
    return ans;
}
int f(int n) {
    if(n==1) return 0;
    int c=phi(n);
    return pow(2,c+f(c),n);
}
int main() {
    dwn(T,read(),1) printf("%d\n",f(read()));
    return 0;
}