2019ICPC网赛南京站B题 super_log（欧拉降幂

https://nanti.jisuanke.com/t/41299

题意：让算a^(a^(a^(...)))，一共b个a, （mod p）的结果。

思路：这是个幂塔函数，用欧拉降幂公式递归求解。

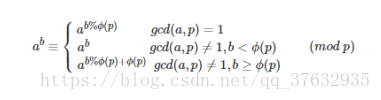
#include<bits/stdc++.h>
#define ll long long
using namespace std;
map<int,int> euler;
ll a,b,mod;
int phi(int n)
{
    int now=n;
    int ret=n;
    if(euler.count(now)) return euler[now];
    for(int i=2;i<=sqrt(n);i++)
    {
        if(n%i==0)
        {
            ret=ret/i*(i-1);
            while(n%i==0)
                n/=i;
        }
    }
    if(n>1)
        ret=ret/n*(n-1);
    euler[now]=ret;
    return ret;
}
ll MOD(ll n,int mod)
{
    return n<mod?n:(n%mod+mod);
}
ll quick_mod(ll base,ll p,int mod)
{
    ll ret=1;
    do{
        if(p&1)
            ret=MOD(base*ret,mod);
        base=MOD(base*base,mod);
    }while(p>>=1);
    return ret;
}
ll solve(int l,int r,int mod)
{
    if(l==r||mod==1) return MOD(a,mod);
    return quick_mod(a,solve(l+1,r,phi(mod)),mod);
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--){
        scanf("%lld%lld%lld",&a,&b,&mod);
        if(a==1||b==0){
            printf("%d\n",1%mod);
            continue;
        }
        if(b==1){
            printf("%d\n",a%mod);
            continue;
        }
        ll ans=solve(1,b,mod)%mod;
        printf("%lld\n",ans);
    }
}