正则化项本质上是一种先验信息,整个最优化问题从贝叶斯观点来看是一种贝叶斯最大后验估计,其中正则化项对应后验估计中的先验信息,损失函数对应后验估计中的似然函数,两者的乘积即对应贝叶斯最大后验估计的形式,如果你将这个贝叶斯最大后验估计的形式取对数,即进行极大似然估计,你就会发现问题立马变成了损失函数+正则化项的最优化问题形式。
在原始的代价函数后面加上一个L1正则化项,即所有权重w的绝对值的和,乘以λ/n:
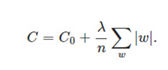
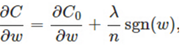
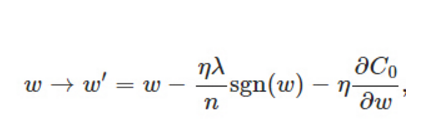
比原始的更新规则多出了η * λ * sgn(w)/n这一项。当w为正时,更新后的w变小。当w为负时,更新后的w变大——因此它的效果就是让w往0靠,使网络中的权重尽可能为0,也就相当于减小了网络复杂度,防止过拟合。当w为0时怎么办?当w等于0时,|W|是不可导的,所以我们只能按照原始的未经正则化的方法去更新w,这就相当于去掉η*λ*sgn(w)/n这一项,所以可以规定sgn(0)=0,这样就把w=0的情况也统一进来了。(在编程的时候,令sgn(0)=0,sgn(w>0)=1,sgn(w<0)=-1)


