伯努利分布是一个离散型机率分布。试验成功，随机变量取值为1；试验失败，随机变量取值为0。成功机率为p，失败机率为q =1-p，N次试验后，成功期望为N*p，方差为N*p*(1-p) ，所以伯努利分布又称两点分布。
观察到的数据为D1，D2，D3，...，DN，极大似然的目标：
联合分布难计算，我们因此引入一个假设，独立同分布（i.i.d.），目标公式改变为：
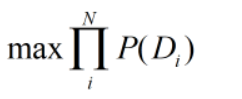
将函数取对数，函数的极值点不会改变，公式变为：
伯努利分布下随机变量的最大似然计算方法，P(X=1)=p，P(X=0)=1-p：
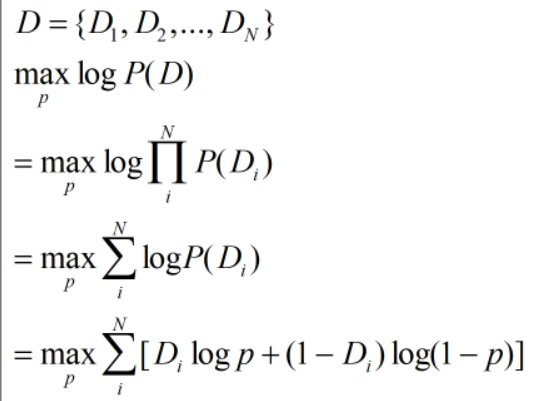
对p求导可得：
令导数为0,得：
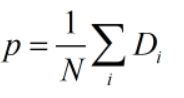
高斯分布下最大似然估计法：
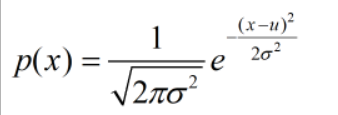
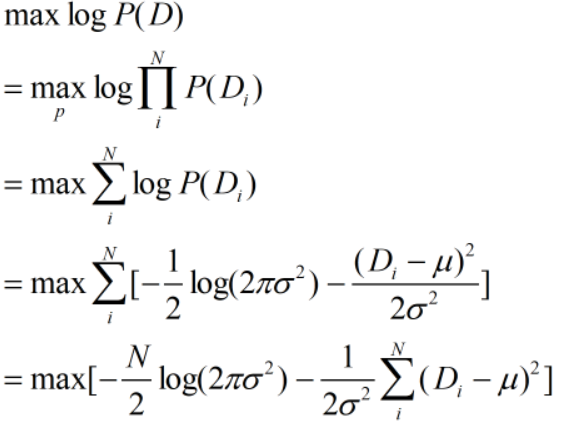
对期望求导：
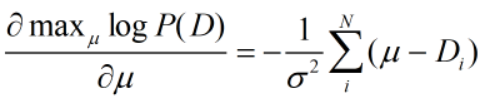
令导数为0：
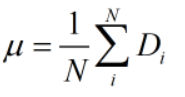
对方差求导，令导数为0：
