[CSP-S模拟测试]:任务分配（最短路+贪心+DP）
题目传送门（内部题149）
输入格式
每个测试点第一行为四个正整数$n,b,s,m$，含义如题目所述。
接下来$m$行，每行三个非负整数$u,v,l$，表示从点$u$到点$v$有一条权值为$l$的有向边，数据保证图是强连通的，也就是任意两个点之间都可以互相走到。
输出格式
对每组数据输出一行一个非负整数表示答案。
样例
样例输入1：
5 4 2 10
5 2 1
2 5 1
3 5 5
4 5 0
1 5 1
2 3 1
3 2 5
2 4 5
2 1 1
3 4 2
样例输出1：
13
样例输入2：
5 4 2 10
5 2 1
2 5 1
3 5 5
4 5 10
1 5 1
2 3 1
3 2 5
2 4 5
2 1 1
3 4 2
样例输出2：
24
数据范围与提示
每个测试点$5$分，各个测试点数据范围如下：
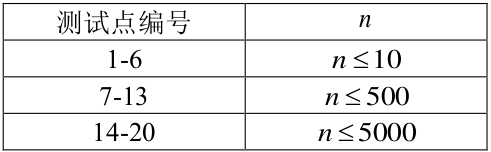
除此之外，数据中可能会均匀出现一些$s$值比较小的点。
对于所有的测试点，均有$m\leqslant 50,000,1\leqslant s\leqslant b<n,0\leqslant l\leqslant 10,000$，给定的有向图合法且强连通。
题解
先求出每个点到总部的正反最短路，建反向边即可。
化一下式子即可发现每一个点的代价为它的正反最短路长度和乘上它所在子项目有几个分部$-1$。
利用贪心的思想，小的放在一起，大的放在一起一定更优，于是可以排个序。
接着考虑$DP$，设$dp[i][j]$表示选到$i$，分了$j$组的最小代价，但是发现时间复杂度是$\Theta(n^3)$的，接着考虑优化。
在最优解中$dis$从小到大依次划分得到的段的长度一定是单调不增的，所以只有$[i-\frac{i}{j},i)$才能更新$dp[i][j]$。
那么现在算法的时间复杂度就是：$\Theta(n^2(\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{n}))=\Theta(n^2\log n)$。
由于时限为$3s$所以跑过去绰绰有余。
时间复杂度：$\Theta(n^2\log n)$。
期望得分：$100$分。
实际得分：$100$分。
代码时刻
#include<bits/stdc++.h>
using namespace std;
struct rec{int nxt,to,w;}e[100001];
int head[2][5001],cnt;
int n,b,s,m;
int dis[2][5001];
bool vis[5001];
long long sum[5001],dp[5001][5001];
priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>>q;
void add(bool id,int x,int y,int w)
{
e[++cnt].nxt=head[id][x];
e[cnt].to=y;
e[cnt].w=w;
head[id][x]=cnt;
}
void Dij0()
{
q.push(make_pair(0,b+1));
dis[0][b+1]=0;
while(q.size())
{
int x=q.top().second;q.pop();
if(vis[x])continue;vis[x]=1;
for(int i=head[0][x];i;i=e[i].nxt)
if(dis[0][e[i].to]>dis[0][x]+e[i].w)
{
dis[0][e[i].to]=dis[0][x]+e[i].w;
q.push(make_pair(dis[0][e[i].to],e[i].to));
}
}
}
void Dij1()
{
memset(vis,0,sizeof(vis));
q.push(make_pair(0,b+1));
dis[1][b+1]=0;
while(q.size())
{
int x=q.top().second;q.pop();
if(vis[x])continue;vis[x]=1;
for(int i=head[1][x];i;i=e[i].nxt)
if(dis[1][e[i].to]>dis[1][x]+e[i].w)
{
dis[1][e[i].to]=dis[1][x]+e[i].w;
q.push(make_pair(dis[1][e[i].to],e[i].to));
}
}
}
int main()
{
scanf("%d%d%d%d",&n,&b,&s,&m);
for(int i=1;i<=m;i++)
{
int a,b,l;
scanf("%d%d%d",&a,&b,&l);
add(0,a,b,l);add(1,b,a,l);
}
memset(dis,0x3f,sizeof(dis));
Dij0();Dij1();
for(int i=1;i<=b;i++)
sum[i]=dis[0][i]+dis[1][i];
sort(sum+1,sum+b+1);
for(int i=1;i<=b;i++)sum[i]+=sum[i-1];
memset(dp,0x3f,sizeof(dp));
dp[0][0]=0;
for(int i=1;i<=b;i++)
for(int j=1;j<=s;j++)
for(int k=i-i/j;k<i;k++)
{
if((sum[i]-sum[k])*(i-k-1)>=dp[i][j])break;
dp[i][j]=min(dp[i][j],dp[k][j-1]+(sum[i]-sum[k])*(i-k-1));
}
printf("%lld",dp[b][s]);
return 0;
}
rp++
