[CSP-S模拟测试]:多维网格(组合数学+容斥)
题目传送门(内部题138)
输入格式
输入数据第一行为两个整数$d,n$。
第二行$d$个非负整数$a_1,a_2,...,a_d$。
接下来$n$行,每行$d$个整数,表示一个坏点的坐标。数据保证坏点在网络范围内,且不会是点$A$或点$B$。
输出格式
一个整数,为从点$A$移动到点$B$的不同的路径数对$10^9+7$取模后的值。
样例
样例输入:
2 1
2 1
1 0
样例输出:
1
数据范围与提示
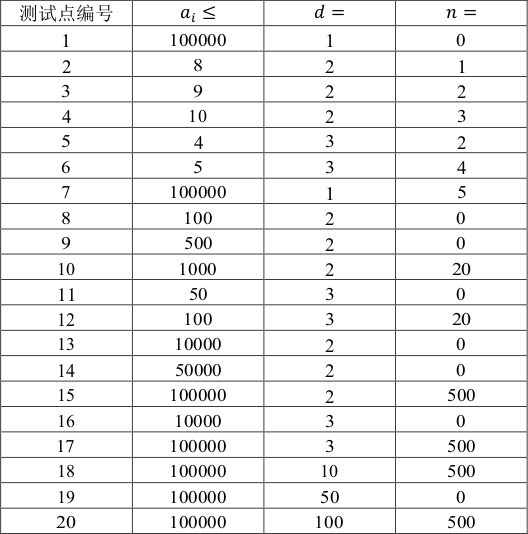
题解
先来考虑$n=0$的情况,利用组合数学,答案就是:
$$ans=(\sum\limits_{i=1}^d a_i)!\times \prod\limits_{i=1}^d(a_i!)^{-1}$$。
再来考虑$n\neq 0$的情况。
考虑容斥。
不妨设$dp[i]$表示从$A$点出发到达$i$点的合法路径条数,$g[i][j]$表示从$i$到$j$的任意路径条数,则有:
$$dp[i]=g[A][i]-\sum\limits_{j=1}^{i-1}dp[j]\times g[j][i]$$
时间复杂度:$\Theta(n^2d)$。
期望得分:$100$分。
实际得分:$100$分。
代码时刻
#include<bits/stdc++.h>
using namespace std;
const int mod=1000000007;
struct rec{int d[101];}a[502];
int d,n;
int fac[10000001],inv[10000001];
long long dp[502];
long long qpow(long long x,long long y)
{
long long res=1;
while(y)
{
if(y&1)res=res*x%mod;
x=x*x%mod;y>>=1;
}
return res;
}
void pre_work()
{
fac[0]=1;
for(int i=1;i<=10000000;i++)fac[i]=1LL*fac[i-1]*i%mod;
inv[10000000]=qpow(fac[10000000],mod-2);
for(int i=10000000;i;i--)inv[i-1]=1LL*inv[i]*i%mod;
}
bool cmp(rec a,rec b){for(int i=1;i<=d;i++)if(a.d[i]!=b.d[i])return a.d[i]<b.d[i];}
long long ask(rec a,rec b)
{
int now=0;
long long res=1;
for(int i=1;i<=d;i++)
{
if(b.d[i]<a.d[i])return 0;
now+=b.d[i]-a.d[i];
res=res*inv[b.d[i]-a.d[i]]%mod;
}
return res*fac[now]%mod;
}
int main()
{
pre_work();scanf("%d%d",&d,&n);
for(int i=1;i<=n+1;i++)
for(int j=1;j<=d;j++)
scanf("%d",&a[i].d[j]);
sort(a+1,a+n+2,cmp);
for(int i=1;i<=n+1;i++)
{
dp[i]=ask(a[0],a[i]);
for(int j=1;j<i;j++)dp[i]=(dp[i]-ask(a[j],a[i])*dp[j]%mod+mod)%mod;
}
printf("%lld",dp[n+1]);
return 0;
}
rp++


 浙公网安备 33010602011771号
浙公网安备 33010602011771号