[CSP-S模拟测试]:小奇的仓库(warehouse)（树形DP）

题目背景

小奇采的矿实在太多了，它准备在喵星系建个矿石仓库。令它无语的是，喵星系的货运飞船引擎还停留在上元时代！

---

题目描述

喵星系有$n$个星球，星球以及星球间的航线形成一棵树。
从星球$a$到星球$b$要花费$[dis(a,b)\ Xor\ M]$秒。（$dis(a,b)$表示$ab$间的航线长度，$Xor$为位运算中的异或）
为了给仓库选址，小奇想知道，星球$i(1\leqslant i\leqslant n)$到其它所有星球花费的时间之和。

---

输入格式

第一行包含两个正整数$n$，$M$。
接下来$n-1$行，每行$3$个正整数$a,b,c$，表示$a$，$b$之间的航线长度为$c$。

---

输出格式

$n$行，每行一个整数，表示星球$i$到其它所有星球花费的时间之和。

---

样例

样例输入：

4 0
1 2 1
1 3 2
1 4 3

样例输出：

6
8
10
12

---

数据范围与提示

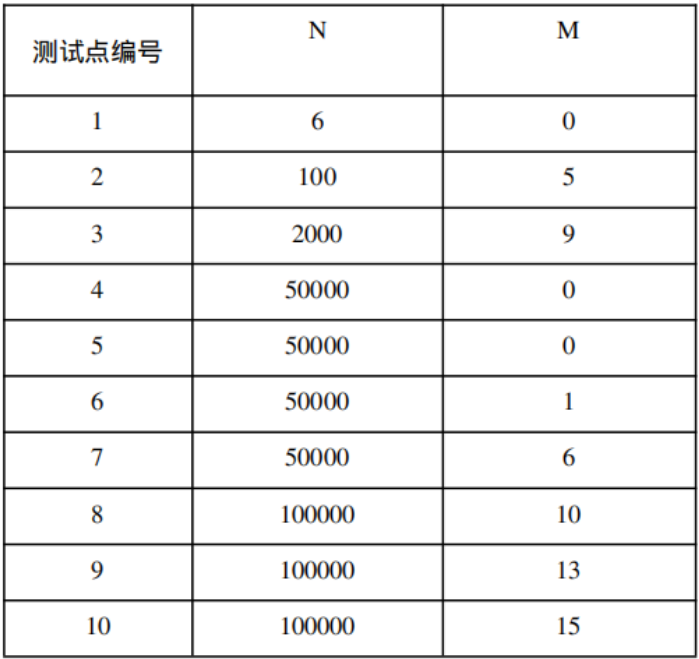
保证答案不超过$2\times {10}^9$。

---

题解

$M=0$的时候的树上$DP$谁都会（假设），那么回归这道题，该怎么办呢？

先来观察数据范围，发现$M$很小，所以依然考虑从$M$入手。

那么我们先来考虑$M=1$的情况，我们只需要在$Xor$的时候记录有多少个$0$，多少个$1$，然后每当一条路径到2，那部分就再记录一个值。

现在来考虑满分算法，我们考虑$0\sim 16$，利用$bitset$不就好啦嘛～

时间复杂度：$\Theta(N\times M)$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
struct rec
{
	int nxt;
	int to;
	int w;
}e[200000];
int head[100001],cnt;
int n,m;
int ans[100001];
int size[100001];
int bit1[100001][20],bit2[100001][20];
long long dp[100001],g[100001];
bool vis[100001];
void add(int x,int y,int w)
{
	e[++cnt].nxt=head[x];
	e[cnt].to=y;
	e[cnt].w=w;
	head[x]=cnt;
}
void dfs(int x)
{
	vis[x]=1;
	bit1[x][0]=size[x]=1;
	for(int i=head[x];i;i=e[i].nxt)
		if(!vis[e[i].to])
		{
			dfs(e[i].to);
			dp[x]+=size[e[i].to]*e[i].w+dp[e[i].to];
			size[x]+=size[e[i].to];
			for(int j=0;j<=15;j++)
				bit1[x][(j+e[i].w)&15]+=bit1[e[i].to][j];
		}
}
void DP(int x,int fa,long long w)
{
	dp[x]=dp[fa];
	dp[x]+=(size[1]-size[x]*2)*w;
	g[x]=dp[x];
	for(int i=0;i<=15;i++)
		bit2[x][(i+w)&15]=bit2[fa][i]+bit1[fa][i]-bit1[x][(i-w+16)&15];
	for(int i=0;i<=15;i++)                  
		g[x]+=(bit2[x][i]+bit1[x][i])*((i^m)-i);
	for(int i=head[x];i;i=e[i].nxt)
		if(e[i].to!=fa)
			DP(e[i].to,x,e[i].w);
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<n;i++)
	{
		int a,b,c;
		scanf("%d%d%d",&a,&b,&c);
		add(a,b,c);
		add(b,a,c);
	}
	dfs(1);
	g[1]=dp[1];
	for(int i=0;i<=15;i++)
		g[1]+=bit1[1][i]*((i^m)-i);
	for(int i=head[1];i;i=e[i].nxt)
		DP(e[i].to,1,e[i].w);
	for(int i=1;i<=n;i++)
		printf("%lld\n",g[i]-m);
	return 0;
}

---

rp++