[BZOJ2208]:[Jsoi2010]连通数(暴力 or bitset or 塔尖?)
题目传送门
题目描述
度量一个有向图连通情况的一个指标是连通数,指图中可达顶点对的个数。
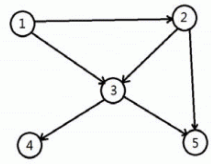
在上图中,顶点1可以到达1、2、3、4、5。
顶点2可以到达2、3、4、5。
顶点3可以到达3、4、5。
顶点4、5均只能到达自身,所以它的连通数为14。
请编写一个程序,输入一个图,求它的连通数。
输入格式
输入数据第一行是图顶点的数量,一个正整数N。 接下来N行,每行N个字符。第i行第j列的1表示顶点i到j有边,0则表示无边。
输出格式
输出一行一个整数,表示该图的连通数。
样例
样例输入:
3
010
001
100
样例输出:
9
数据范围与提示
对于100%的数据,N不超过2000。
题解
千万不要以为这道题数据范围N≤2000就可以暴力,N≤2000意味着最多会有$N^{2}$条边,dfs一遍遍历时间复杂度为边数,那么这道题就会被卡成$N^{3}$。
不过由于数据比较水,暴力卡常也可以A掉……

然而,占用评测资源显然是一种rp--的行为,所以考虑优化。
bitset!!!
利用floyed的思想。

空间和时间都在很大程度上得到了优化。
还不够快?
考虑塔尖缩点,一个强联通分量缩成一个点之后只要经过这个点,它里面的点都能被经过,所以记录size即可。

好吧,典型的空间换时间……
代码时刻
暴力:
#include<bits/stdc++.h>
using namespace std;
struct rec
{
int nxt;
int to;
}e[4000000];
int head[2001],cnt;
bool vis[2001];
long long ans;
char ch[2001];
void add(register int x,register int y)
{
e[++cnt].nxt=head[x];
e[cnt].to=y;
head[x]=cnt;
}
void dfs(register int x)
{
vis[x]=1;
ans++;
for(register int i=head[x];i;i=e[i].nxt)
if(!vis[e[i].to])dfs(e[i].to);
}
int main()
{
int n;
scanf("%d",&n);
for(register int i=1;i<=n;i++)
{
scanf("%s",ch+1);
for(register int j=1;j<=n;j++)if(ch[j]=='1')add(i,j);
}
for(register int i=1;i<=n;i++)memset(vis,0,sizeof(vis)),dfs(i);
printf("%d",ans);
return 0;
}
//推荐使用register进行卡常,评测机稍卡都有可能过不了,然而我5分钟1A了……
bitset优化:
#include<bits/stdc++.h>
using namespace std;
char ch[2001];
bitset<2001> a[2001];//bitset
int ans;
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%s",ch+1);
for(int j=1;j<=n;j++)
if(ch[j]=='1')a[i][j]=1;
a[i][i]=1;
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(a[j][i])a[j]|=a[i];//运用floyed思想
for(int i=1;i<=n;i++)ans+=a[i].count();//统计答案
cout<<ans<<endl;
return 0;
}
//我觉得代码好小巧,你觉得呢?
塔尖+bitset:
#include<bits/stdc++.h>
using namespace std;
struct rec
{
int nxt;
int to;
}e[4000000],wzc[4000000];
int n;
int head[2001],cnt;
int headw[2001],cntw;
long long ans;
char ch[2001];
int dfn[2001],low[2001],sta[2001],ins[2001],c[2001],size[2001],num,top,tot;
int que[2001],d[2001],lft=1,rht=1;
bitset<2001> a[2001];
void add(int x,int y)//旧图
{
e[++cnt].nxt=head[x];
e[cnt].to=y;
head[x]=cnt;
}
void add_w(int x,int y)//新图
{
wzc[++cntw].nxt=headw[x];
wzc[cntw].to=y;
headw[x]=cntw;
}
void tarjan(int x)//缩点
{
dfn[x]=low[x]=++num;
sta[++top]=x;
ins[x]=1;
for(int i=head[x];i;i=e[i].nxt)
{
if(!dfn[e[i].to])
{
tarjan(e[i].to);
low[x]=min(low[x],low[e[i].to]);
}
else if(ins[e[i].to])
low[x]=min(low[x],dfn[e[i].to]);
}
if(dfn[x]==low[x])
{
tot++;
int y;
do
{
y=sta[top--];
ins[y]=0;
c[y]=tot;
size[tot]++;
}while(x!=y);
}
}
void build()//建新图
{
for(int x=1;x<=n;x++)
for(int i=head[x];i;i=e[i].nxt)
if(c[x]!=c[e[i].to])
{
add_w(c[x],c[e[i].to]);
d[c[e[i].to]]++;
}
}
void _doudou()//统计答案
{
for(int i=1;i<=tot;i++)
if(!d[i])que[++rht]=i;
while(lft<=rht)
{
a[que[lft]][que[lft]]=1;
for(int i=headw[que[lft]];i;i=wzc[i].nxt)
{
a[wzc[i].to]|=a[que[lft]];
d[wzc[i].to]--;
if(!d[wzc[i].to])que[++rht]=wzc[i].to;
}
lft++;
}
for(int i=1;i<=tot;i++)
for(int j=1;j<=tot;j++)
if(a[i][j])ans+=size[i]*size[j];
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%s",ch+1);
for(int j=1;j<=n;j++)if(ch[j]=='1')add(i,j);
}
for(int i=1;i<=n;i++)
if(!dfn[i])tarjan(i);
build();
_doudou();
printf("%d",ans);
return 0;
}
//比较恶心,考试的时候建议使用前两种做法,这种做法仅供参考和装逼……
rp++

