AC自动机讲解+[HDU2222]:Keywords Search(AC自动机)
引入
首先,有这样一道题:
给你一个单词W和一个文章T,问W在T中出现了几次(原题见POJ3461)。
OK,so easy~
HASH or KMP 轻松解决。
那么还有一道例题:
给定n个长度不超过50的由小写英文字母组成的单词准备查询,以及一篇长为m的文章,问:文中出现了多少个待查询的单词(原题见POJ3630)。
OK,依然so easy~
字典树(Trie)轻松解决。
那么,如果你说,什么是KMP和Trie,那么恭喜你啊……
建议大家要在看这篇博客之前做到:
进阶
如果你能看到这里,说明你已经熟练掌握了Trie和KMP。
那么现在可爱的动动扔给你了一道题:
给定n个长度不超过50的由小写英文字母组成的单词准备查询,以及一篇长为m的文章,问:文中出现了多少个待查询的单词。多组数据。

那么这个时候需要引入一个新的算法:AC自动机。
想必在所得诸位大佬一定有人听过这个名词。
首先简要介绍一下AC自动机(Aho-Corasick automation)(不是Accepted)。
就像当初我前队友gzh老师一样(状压 or 撞鸭?)。
该算法在1975年产生于贝尔实验室,是著名的多模匹配算法之一。
要搞懂AC自动机,先得有模式树(字典树)Trie和KMP模式匹配算法的基础知识。
KMP算法和AC自动机算法的区别在于,前者为单模式串匹配,而后者为多模式串匹配。
你可以感性的理解为,单模式串匹配就是只有一个子串,而多模式串匹配是指有不止一个子串。
主要步骤
三步走:
①将所有的模式串构成一颗Trie树。
②对Trie上所有的节点构造前缀指针。
③利用前缀指针Fail对主串进行匹配。
实际上这个前缀指针Fail与KMP算法中的nxt数组非常相似,因此AC自动机可以看作是Trie与KMP算法的结合(Trie上的KMP算法)。

第一步:字典树的构建想必大家都会了(如果不会的话你也不会读到这里),在此就不做过多的赘述。
第二步:
找Fail指针:
大家都知道,在KMP算法当中,当字符串发生失配时有nxt数组用来找到下一个匹配的位置,那么AC自动机中类似nxt数组的东西就是Fail指针,当发现失配的
字符失配的时候,跳转到Fail指针指向的位置,然后再次进行匹配操作,AC自动机之所以能实现多模式匹配,就归功于Fail指针的建立。
那么我们应该如何求Fail指针呢?
运用广度优先搜索 (BFS)来求得。
对于与根节点直接相连的点来说,如果这些节点失配,他们的Fail指针直接指向root即可。
其他节点其Fail指针求法如下:
设当前节点为father,其子节点为child。
求child的Fail指针时,首先我们要找到其father的Fail指针所指向的节点设为F,看F的孩子中有没有和child节点所表示的字母相同的节点,如果有的话,这个节
点就是child的Fail指针,如果没有,则需要再找到F的Fail指针所指向的节点,如果一直找都找不到,则child的Fail指针就要指向root。
例(帮助理解):
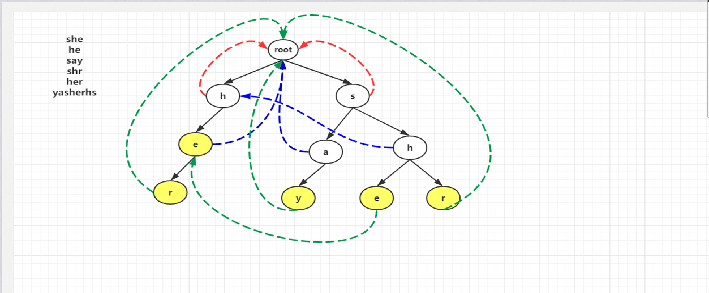
如图所示,首先root最初会进队,然后root,出队,我们把root的孩子的失败指针都指向root。因此图中h,s的失败指针都指向root,如红色线条所示,同时h,s进队。
接下来该h出队,我们就找h的孩子的Fail指针,首先我们发现h这个节点其Fail指针指向root,而root又没有字符为e的孩子,则e的Fail指针是空的,如果为空,则也要指向root,如图中蓝色线所示。并且e进队,此时s要出队,我们再找s的孩子a,h的Fail指针,我们发现s的Fail指针指向root,而root没有字符为a的孩子,故a的Fail指针指向root,a入队,然后找h的Fail指针,同样的先看s的Fail指针是root,发现root又字符为h的孩子,所以h的Fail指针就指向了第二层的h节点。e,a , h 的Fail指针的指向如图蓝色线所示。
此时队列中有e,a,h,e先出队,找e的孩子r的失败指针,我们先看e的失败指针,发现找到了root,root没有字符为r的孩子,则r的失败指针指向了root,并且r进队,然后a出队,我们也是先看a的失败指针,发现是root,则y的fail指针就会指向root.并且y进队。然后h出队,考虑h的孩子e,则我们看h的失败指针,指向第二层的h节点,看这个节点发现有字符值为e的节点,最后一行的节点e的失败指针就指向第三层的e。最后找r的指针,同样看第二层的h节点,其孩子节点不含有字符r,则会继续往前找h的失败指针找到了根,根下面的孩子节点也不存在有字符r,则最后r就指向根节点,最后一行节点的Fail指针如绿色虚线所示。
第三步:
文本串的匹配:
匹配过程分两种情况:
(1)当前字符匹配,从当前节点沿着树边有一条路径可以到达目标字符,如果当前匹配的字符是一个单词的结尾,就沿着当前字符的Fail指针,一直遍历到根,如果这些节点末尾有标记(当前节点单词末尾的标记),这些节点全都是可以匹配上的节点。统计完毕后,并将那些节点标记。此时只需沿该路径走向下一个节点继续匹配即可,目标字符串指针移向下个字符继续匹配;
(2)当前字符不匹配,则去当前节点失败指针所指向的字符继续匹配,当指针指向root时结束。
重复这2个过程中的任意一个,直到模式串走到结尾为止。
例:
还是刚才那张图:

假设其模式串为yasherhs。对于i=0,1。Trie中没有对应的路径,故不做任何操作;i=2,3,4时,指针p走到左下节点e。因为节点e的count信息为1,所以cnt+1,并且讲节点e的count值设置为-1,表示改单词已经出现过了,防止重复计数,最后temp指向e节点的失败指针所指向的节点继续查找,以此类推,最后temp指向root,退出while循环,这个过程中count增加了2。表示找到了2个单词she和he。当i=5时,程序进入第5行,p指向其失败指针的节点,也就是右边那个e节点,随后在第6行指向r节点,r节点的count值为1,从而count+1,循环直到temp指向root为止。最后i=6,7时,找不到任何匹配,匹配过程结束。
总结
三步:构造一棵Trie树,构造失败指针和模式匹配过程。
Fail指针≈nxt数组。
例题
「一本通 2.4 例 1」Keywords Search
「一本通 2.4 练习 1」玄武密码
「一本通 2.4 练习 3」单词
「一本通 2.4 练习 5」病毒
「一本通 2.4 练习 4」最短母串
「一本通 2.4 练习 6」文本生成器
例题1讲解
那么下面我来讲一下AC自动机的第一道例题Keywords Search。
这是一道板子题,其实上面的内容就是根据这道题来讲的,我在此就不做过多的赘述,主要讲一下代码。
#include<bits/stdc++.h>
using namespace std;
int n;
char s[2000001];
int trie[1000001][30];
int que[1000001],end[1000001],nxt[1000001];
int ans,cnt;
void insert(char *str)//Trie树构建过程
{
int p=1;
int len=strlen(str);
for(int i=0;i<len;i++)
{
int ch=str[i]-'a';
if(!trie[p][ch])
{
trie[p][ch]=++cnt;
memset(trie[cnt],0,sizeof(trie[cnt]));//每次只需要清空我们会用得到的行
}
p=trie[p][ch];
}
end[p]++;//因为有可能会有重复的单词,故在此end统计在此有多少个单词结束,而不是有没有单词结束
}
void build()//BFS构建Fail指针
{
for(int i=0;i<26;i++)//为了方便将0的所有转一遍都设为根节点1
trie[0][i]=1;
nxt[1]=0;//若在根节点失配, 则无法匹配字符
que[1]=1;
int head=1,tail=1;
while(head<=tail)
{
for(int i=0;i<26;i++)
if(!trie[que[head]][i])trie[que[head]][i]=trie[nxt[que[head]]][i];//注意这里,下面会有详细解释
else
{
que[++tail]=trie[que[head]][i];
int flag=nxt[que[head]];
while(flag&&!trie[flag][i])flag=nxt[flag];//循环往前找
nxt[trie[que[head]][i]]=trie[flag][i];
}
head++;//注意队头++
}
}
void find(char *str)//匹配
{
int p=1;
int len=strlen(str);
for(int i=0;i<len;i++)
{
int flag=p=trie[p][str[i]-'a'];
while(end[flag]!=-1&&flag)
{
ans+=end[flag];
end[flag]=-1;//标记这个点已经访问过,以后不再访问
flag=nxt[flag];
}
}
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
memset(end,0,sizeof(end));//多测不清空,爆零两行泪(宝宝别哭)
cnt=1;
ans=0;
for(int i=0;i<26;i++)
trie[0][i]=1,trie[1][i]=0;//亦是清空
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%s",s);
insert(s);//读入子串并插入Trie树
}
build();
scanf("%s",s);
find(s);//匹配
printf("%d\n",ans);
}
return 0;
}
下面我来解释上面那个问题:
当发现不存在que[head](下面用u代替)的转移边i时,令trie[u][i]等于trie[nxt[u]][i],这并不符合Trie树的构造,但是在代码中却是正确的,那么这是为什么呢?
其实这是为了优化时间,若不存在trie[u][i]的转移边则指向trie[nxt[u]][i]。因为在具体问题中,若不存在trie[u][i]的转移边,往往需要沿que[head]的Fail指针走到第一个满足存在字符i的转移边的点v,得到trie[v][i],那么就直接将trie[u][i]赋值为trie[v][i],即trie[nxt[u]][i],这是求解的一类问题的时间优化。也正是这个原因,在构建Fail指针是,并没有处理v的转移边i不存在的情况,而是直接nxt[trie[u][i]]=trie[v][i](其中trie[v][i]也在之前就处理好了)。
rp++


 浙公网安备 33010602011771号
浙公网安备 33010602011771号