CART(Classification and Regression Trees)
CART(Classification and Regression Trees)是一种常用的决策树算法,既可以用于分类问题,也可以用于回归问题。CART算法由Breiman等人于1984年提出,是一种基于递归二分划分的贪婪算法。以下是对CART算法的详细解释:
1. 决策树的构建过程:
CART算法通过递归地将数据集划分为越来越纯的子集,构建一棵二叉树。具体过程如下:
- 选择最佳分裂特征:
- 对于分类问题,通常使用基尼指数(Gini Index)作为评价指标;对于回归问题,通常使用平方误差(Squared Error)。
- 遍历每个特征,每个可能的分裂点,计算分裂后子集的基尼指数或平方误差,选择使指标最小化的特征和分裂点作为当前节点的分裂规则。
- 递归分裂:
- 根据选择的分裂规则将数据集划分为两个子集,分别对这两个子集递归地应用上述过程,构建左右子树。
- 停止条件:
- 递归的停止条件通常包括:
- 达到最大深度。
- 节点中的样本数量小于某个阈值。
- 基尼指数或平方误差小于某个阈值。
- 递归的停止条件通常包括:
2. CART用于分类问题的基尼指数:
对于一个具有K个类别的分类问题,节点的基尼指数(Gini Index)的计算方式为:
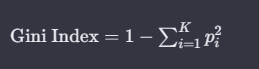
其中 是属于第 个类别的样本在节点中的比例。基尼指数越小,节点的纯度越高。
3. CART用于回归问题的平方误差:
对于回归问题,节点的平方误差(Squared Error)的计算方式为:
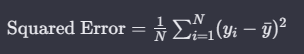


 浙公网安备 33010602011771号
浙公网安备 33010602011771号