简聊DFA（确定性有限状态自动机）

状态机理论最初的发展在数字电路设计领域。而在软件设计领域，状态机设计的理论俨然已经自成一体。

状态机是软件编程中的一个重要概念，比这个概念更重要的是对它的灵活应用。在一个思路清晰而且高效的程序中，必然有状态机的身影浮现。比如说一个按键命令解析程序，就可以被看做状态机：本来在A状态下，触发一个按键后切换到了B状态，再触发另一个键后切换到C状态，或者返回到A状态。这就是最简单的按键状态机例子。实际的按键解析程序会比这更复杂些，但这不影响我们对状态机的认识。进一步看，击键动作本身也可以看做一个状态机。一个细小的击键动作包含了：释放、抖动、闭合、抖动和重新释放等状态。

1. 状态机的历史

纯属个人观点，如有错误请指正

状态机衍生于离散数学中的图论，然后针对于特定场景下提出的延伸性概念。
图论最开始研究的是现实中的事物之间的关系。
比如图论里面经典的“七桥问题”，是有具体的事物：4个岛屿，7座桥梁。

随着科技的进步，发现一些新的事情无法用“事物”来表述。
而计算机程序的状态机则更加抽象了“事物”的概念，“状态”即“事物”。“状态”可以对应独立事物的状态，如人的状态：开心，悲伤，严肃，正常等；也可以对应多种事物间的关系，如我爱你，你爱他，他爱我。
我们也把多种事物的状态抽象成一个独立的整体，比如“三角恋”，可以当做一个独立的整体来研究。

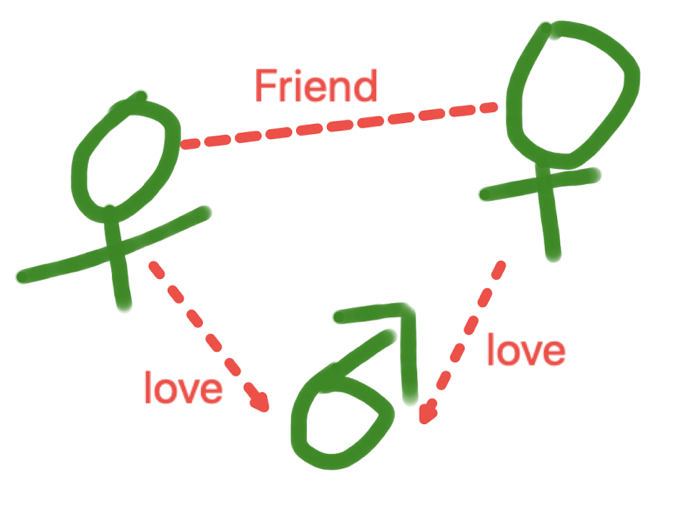
其实很多时候我们延伸了状态的概念，比如数据，或者关系

2.概念

无限状态机属于理论上的一个模型，比如人脑，对于目前人类来说就属于无限状态机。
现在的人工智能AI，理论上是要实现的就应该是无限状态机。可以在任何情况下，做出合理的抉择。
而目前人工智能无法“打败”人类，也是因为状态是可以被枚举的。

不可预测是无限状态机么？

我们主要来研究有限状态机：状态可以被枚举的状态机。先来统一几个概念：

• 输入：有可能触发状态改变的 数据、事件等；每个节点都必须至少有一个输入；
• 转换：从一种状态转移到另一种状态之间的过程；“状态”被转换以后，可能是一种新态，也可能不变；
• 状态：从某种维度建立的，描述当前系统、事物等的数据；
• 接受状态（终态）：被用户接受的状态；
• 非接受状态：中间状态，不被用户接受，但现实存在的状态；

我们要说明的是DFA，即确定性有穷状态自动机：在输入一个状态时，只得到一个固定的状态。

3. 一个简单的DFA

人抽烟生病：

• 正常状态A

• 难受状态B

• 住院状态C

• h：普通抽一支，没事儿，还是A；

• i： 抽多了，开始不舒服B；

• j：检查出来生病了，肺部损伤住院C；

• k：赶紧拿掉药，猛吃；

• l：开始好转，回到默认状态；
  此时回到了A（正常）状态；

下图的状态演示图里面，表明这个烟民没有戒烟成功，还是在向C状态转移。

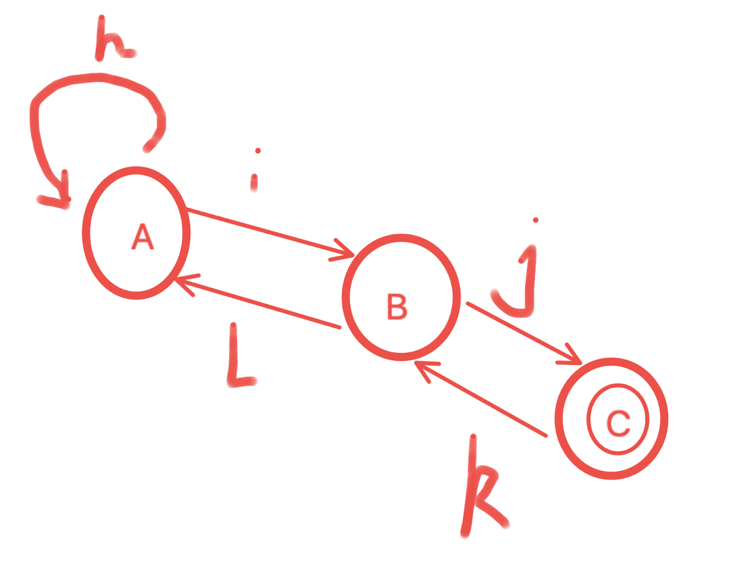
其中：
输入： h ,i ,j,k,l
转换： 箭头连线
状态：A，B，C
非接受态：A,B
接受态：C

我们用数学符号表示：

• M = (Q,Σ,𝛿 )
• Q：有限状态集合(如 {A,B,C})
• Σ: 有限输入集合(如{ h,i,j,k,l})
• 𝛿 : 状态转换步骤(如 有向箭头）

为了更进一步区分：

• M = (Q,Σ,𝛿 ,q0,F)
• q0: 初始态（如A)
• F: 接受态集合(如{C})

在状态机的图里面，我们约定：

• 一个圆圈代表 非接受态
• 两个圆圈代表 接受态
• 箭头代表转换函数
• 箭头字符表示输入的数据、事件

4.实现状态机

状态机主要实现三大要素，
输入，
转换，
状态。

/*
M = (Q,Σ,𝛿 ,q0,F)
Q(别名State,简写 S)： 有限状态集合(如 {A,B,C})
Σ:  有限输入集合(如{ h,i,j,k,l}),外部输入
𝛿（别名 Input,简写I) : 状态转换步骤(如 有向箭头）
q0: 初始态（如A)
F: 接受态集合(如{C})

！！！！通过输入驱动的状态机！！！
 */
export interface DFATransition<S> {

    /** 前置态 */
    from: S;

    /** 目标态 */
    to: S;

    /** 目标状态的执行函数 */
    toFunc: Function;
}

export class DFA<S, I extends string, T extends DFATransition<S>> {

    /**
     * 初始状态
     */
    private startState: S = null;

    /**
     * 当前状态
     */
    private _curState: S = null;

    /**
     * 接受态（最终态）
     */
    private acceptState: S[] = [];

    /**
     * 状态切换函数𝛿
     */
    private transMap: Map<I, T[]> = new Map();

    /**
     * 所有状态集合S
     */
    private stateSet: Set<S> = new Set();

    /**
     * 所有输入集合Σ
     */
    private inputSet: Set<I> = new Set();

    constructor(state: S, acceptState: S[]) {
        this.startState = state;
        this.acceptState = acceptState;
        this.resetStart();
    }
    get curState(): S {
        return this._curState;
    }
    set curState(s: S) {
        console.log('[DFA]DFA设置到状态：', s);
        this._curState = s;
    }

    /**
     * 恢复初始状态
     */
    public resetStart(): void {
        this.curState = this.startState;
    }

    /**
     * 创建状态机执行结构;
     * 如果已经存在当前结构，则覆盖：
     *      比如，从 a->b已经存在了，这次再次添加，则a->b被覆盖；
     * @param from 开始态
     * @param to 目标态
     * @param input 转换条件、事件
     * @param toFunc 目标态对应的执行器
     * @returns 
     */
    public add = (from: S, to: S, input: I, toFunc: Function): DFA<S, I, T> => {
        // FIXME 不用as T会报错
        let newT = { from, to, toFunc } as T;
        let arr: T[] = this.transMap.get(input);
        if (!arr) {
            arr = [];
            this.transMap.set(input, arr);
        }
        // HACK 效率不高，看着好看,[]也会被执行一遍
        let hasCover = false;
        for (let i = 0, len = arr.length; i < len; i++) {
            let t = arr[i];
            if (t.from === from) {
                // 为什么没有判断 t.to == to? 因为转移的条件是 状态+输入，目标状态是确定的；如果加入to，可能能 输入i+状态s -》可能会对应不同的结果；
                // 如果存在当前转移
                arr[i] = newT;
                hasCover = true;
            }
        }
        if (!hasCover) {
            arr.push(newT);
        }
        this.stateSet.add(from).add(to);
        this.inputSet.add(input);
        return this;
    }

    /**
     * 事件输入
     * @param i 
     */
    public input = (i: I): boolean => {
        let arr: T[] = this.transMap.get(i);
        let t: T = null;
        if (arr && arr.length) {
            // 找到当前转移
            arr.some((item: T) => {
                if (item.from === this.curState) {
                    t = item;
                    console.log('[DFA]DFA转移，起始态：' + t.from + '终止态：' + t.to);
                    this.curState = item.to;
                    item.toFunc && item.toFunc();
                    return true;
                }
            });
        }
        if (!t) {
            console.log('[DFA]DFA无法响应输入事件，无法处理当前转移类型：' + i, '当前状态：' + this.curState);
            return false;
        } else {
            return true;
        }
    }

    /**
     * 当前状态机是否存在对应的状态
     * @param s 被判断的状态
     * @returns 
     */
    public hasState(s: S): boolean {
        return this.stateSet.has(s);
    }

    public getStateLen(): number {
        return this.stateSet.size;
    }

    /**
     * 
     * @returns 是否是初始态
     */
    public isStartState = (): boolean => this.curState === this.startState

    /**
     * 
     * @returns 当前状态是否被接受
     */
    public canAccept = (): boolean => this.acceptState.includes(this.curState)
}

4. 状态机与状态模式

都有“状态”。

状态机是建模方式，是一种模型；
状态模式是基于状态改变行为的设计模式,表示状态的行为。

5. 应用场景

在项目中尝试用状态机制作触摸。
触摸包含 ：开始触摸，touchBegin；触摸移动，touchMove; 触摸结束，touchEnd
其中，点击事件是 touchBegin+touchEnd

实现以后，发现代码非常难维护；比如当前物件既有拖动，又有点击的时候，很难去清晰的进行状态转移。会新增一些hack写法。

6.总结

个人认为状态机思想是惊为天人的，在一些领域有重要意义。而在前端交互上，用状态机实现一些东西，容易出现各种问题：
如：设置“伪态”；他人难以维护；新增状态时需要非常谨慎。
大多数场景下，我们不一定要用他，通过别的方式也可以实现。
内心一定要有它！！！

参考：

自动机，状态机，有限自动机，有限状态机，有限状态自动机，非确定下有限状态自动，确定性有限状态自动机的区别于联系
http://www.voidcn.com/article/p-bgmycagl-de.html
谈谈状态机
https://zhuanlan.zhihu.com/p/28142401
编译原理笔记3：有限自动机
https://www.jianshu.com/p/afad52d4c5d4
证明与计算(7): 有限状态机(Finite State Machine)
https://www.cnblogs.com/math/p/fsm.html
浅谈状态机原理及其应用
https://blog.csdn.net/zhuqiuhui/article/details/102533721?utm_medium=distribute.pc_relevant_download.none-task-blog-baidujs-2.nonecase&depth_1-utm_source=distribute.pc_relevant_download.none-task-blog-baidujs-2.nonecase
【翻译】游戏设计模式之状态机
https://zhuanlan.zhihu.com/p/74984237
游戏状态机实现介绍
https://blog.csdn.net/yonshi/article/details/40082021
技术系列之“状态机”
https://kb.cnblogs.com/page/528966/
状态机思路在程序设计中的应用
https://kb.cnblogs.com/page/528971/
《有限状态机在开放式数控系统中的应用》