分类模型效果评估
分类模型效果评估
评估标准:
- Accuracy
- Precision
- Recal
- F Score
- ROC curve
以鸢尾花数据集为例子,我们用PCA(主成分回归法)(重点展示效果评估这一块,所以暂时只用这一方法选择特征)绛维,然后进行建模,最后对模型的效果进行评估。
import pandas as pd
import numpy as np
from sklearn.decomposition import PCA
iris = pd.read_csv(r"G:\Iris_copy.csv")
iris.sample(4)
| Id | SepalLengthCm | SepalWidthCm | PetalLengthCm | PetalWidthCm | Species | |
|---|---|---|---|---|---|---|
| 48 | 49 | 5.3 | 3.7 | 1.5 | 0.2 | 0 |
| 75 | 76 | 6.6 | 3.0 | 4.4 | 1.4 | 1 |
| 128 | 129 | 6.4 | 2.8 | 5.6 | 2.1 | 2 |
| 84 | 85 | 5.4 | 3.0 | 4.5 | 1.5 | 1 |
del iris["Id"]
iris.sample(3)
| SepalLengthCm | SepalWidthCm | PetalLengthCm | PetalWidthCm | Species | |
|---|---|---|---|---|---|
| 114 | 5.8 | 2.8 | 5.1 | 2.4 | 2 |
| 92 | 5.8 | 2.6 | 4.0 | 1.2 | 1 |
| 77 | 6.7 | 3.0 | 5.0 | 1.7 | 1 |
data = iris.iloc[:,:4]
data.head(3)
| SepalLengthCm | SepalWidthCm | PetalLengthCm | PetalWidthCm | |
|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 |
pca = PCA() #先保留所有成分
pca.fit(data)
print(pca.explained_variance_)
print("各个成分的方差百分比(贡献率):", pca.explained_variance_ratio_)
[ 4.22484077 0.24224357 0.07852391 0.02368303]
各个成分的方差百分比(贡献率): [ 0.92461621 0.05301557 0.01718514 0.00518309]
当选取前两个主成分时,累计贡献率已达97.76%。接下来保留两个主成分。
pca = PCA(2)
pca.fit(data)
new_data = pca.transform(data) #转换原始数据
new_data = pd.DataFrame(new_data)
Species = pd.DataFrame(iris.Species)
new_iris = pd.concat([new_data, Species], axis=1) #拼接数据
print(new_iris.head())
0 1 Species
0 -2.684207 0.326607 0
1 -2.715391 -0.169557 0
2 -2.889820 -0.137346 0
3 -2.746437 -0.311124 0
4 -2.728593 0.333925 0
下面用逻辑回归来进行建模
from sklearn.linear_model import LogisticRegression as LR
from sklearn.model_selection import train_test_split
x = new_iris.iloc[:,:2]
y = new_iris.iloc[:,-1]
x_train, x_test, y_train, y_test = train_test_split(x,y,test_size=0.3)
lr = LR()
lr.fit(x_train,y_train)
y_pred = lr.predict(x_test)
接下来介绍几种模型效果的评测标准

1.混淆矩阵
Actual = [1,1,0,0,1,0,0,0,1,1]
Model = [0,0,0,1,1,1,1,0,0,0]
from sklearn.metrics import confusion_matrix
a = confusion_matrix(Actual, Model)
b = pd.DataFrame(a,columns=["0","1"],index=["0","1"])
b.index.name = "实际"
b.columns.name = "模型"
b
| 模型 | 0 | 1 |
|---|---|---|
| 实际 | ||
| 0 | 2 | 3 |
| 1 | 4 | 1 |
二分类中
TP,预测是正样本实际是正样本,预测正确
FP,预测是正样本实际是负样本,预测错误
FN,预测是负样本实际是正样本,预测错误
TN,预测是负样本实际是负样本,预测正确
from sklearn.metrics import confusion_matrix
confusion_matrix(y_test,y_pred)
array([[16, 0, 0],
[ 0, 11, 5],
[ 0, 0, 13]], dtype=int64)
2.Accuracy (准确率)
Accuracy = (TP+TF)/(TP+FP+FN+TN)
Accuracy是对分类器整体上的正确率的评价,而Precision是分类器预测为某一个类别的正确率的评价。
Accuracy要在样本均衡时使用才有效 ,不然再高也不能代表该模型好。
例:我买了100000个玩具,其中100个是Bubblebee,其余的是海绵宝宝,现在我想把
Bubblebee全部放在客厅。我让一个小朋友帮我忙,那即使他把这100000个玩具都判定为海绵宝宝,那他的判断能力
Accuracy = (TP+TF)/(TP+FP+FN+TN)
=(0+99900)/100000
= 99.9%
这么高的Accuracy却依然没有真实反映这个小朋友的判断能力。Consequently,在实际应用中,若样本不均衡,不能仅以Accuracy为模型的评判标准。
要加以考虑下面的评判标准。
3.Precision (精准率)
Precision = TP/(TP+FP)
在所有预测为正的样本中,实际为正的样本比例 (猜对率)
4.Recall (召回率)
Recall = TP/(TP+FN)
在所有实际为正的样本中,预测为正的比例 (猜全率)
**5.F1-score **
精确率和召回率是相互制约的,一般精确率低的召回率高,精确率搞得召回率低。所以出现了f1 score,它是 Precision 和 Recall 的调和平均数。
F1-score = 2 / [(1 / precision) + (1 / recall)]
Fscore里的一个检验值
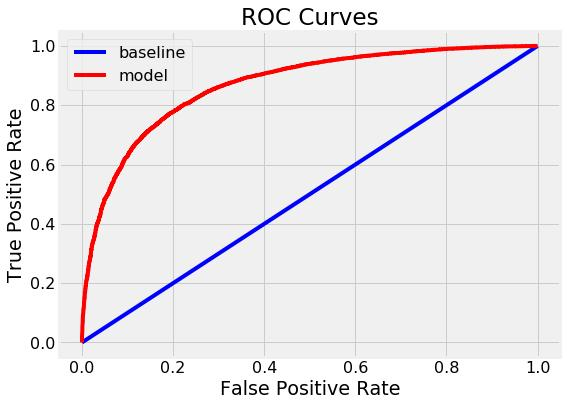
6.Roc/Auc (仅针对二分类变量)
ROC 是针对不同阈值,根据对应的fpr、tpr生成ROC图,曲线下方的面积就是AUC(类似散点图跟相关系数的关系,一者以图的形式给你直观感受,一者以精确的尺度衡量大小)
横坐标fpr (tpr是模型在正样本上的预测准确率)
纵坐标tpr(fpr是模型在负样本上的预测准确率)
fpr, tpr, thresholds = metrics.roc_curve(y_test,y_pred)
import matplotlib.pyplot as plt
plt.plot(fpr, tpr)
auc_value = auc(fpr,tpr) #计算auc值
官网参考:https://scikit-learn.org/stable/modules/generated/sklearn.metrics.roc_curve.html
sklearn.metrics.roc_curve(y_true, y_score, pos_label=None, sample_weight=None, drop_intermediate=True)[source]¶
仅针对二分类变量
""""""
Parameters:
y_true : array, shape = [n_samples]
实际的二分类标签. 如果标签不是 {-1, 1} 或者 {0, 1}, 那么pos_label应该被指定,表示哪个是正标签,剩下的那个就是负标签。
y_score : array, shape = [n_samples]
Target scores, 也可以是正类标签的估计概率, confidence values, or non-thresholded measure of decisions (as returned by “decision_function” on some classifiers).
pos_label : int or str, default=None
Label considered as positive and others are considered negative.
sample_weight : array-like of shape = [n_samples], optional
Sample weights.
drop_intermediate : boolean, optional (default=True)
Whether to drop some suboptimal thresholds which would not appear on a plotted ROC curve. This is useful in order to create lighter ROC curves.
New in version 0.17: parameter drop_intermediate.
Returns:
fpr : array, shape = [>2]
Increasing false positive rates such that element i is the false positive rate of predictions with score >= thresholds[i].
tpr : array, shape = [>2]
Increasing true positive rates such that element i is the true positive rate of predictions with score >= thresholds[i].
thresholds : array, shape = [n_thresholds]
Decreasing thresholds on the decision function used to compute fpr and tpr. thresholds[0] represents no instances being predicted and is arbitrarily set to max(y_score) + 1.
""""""
#后面再翻译
And then,实践:
from sklearn import metrics
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))
print("Precision:",metrics.precision_score(y_test, y_pred, average='micro'))
print("Recall:",metrics.recall_score(y_test, y_pred, average='micro'))
print("f1-score:",metrics.f1_score(y_test, y_pred, average='micro'))
Accuracy: 0.888888888889
Precision: 0.888888888889
Recall: 0.888888888889
f1-score: 0.888888888889
classification_report直接把上面的指标综合成一份报告输出:
from sklearn.metrics import classification_report
print(classification_report(y_test,y_pred))
precision recall f1-score support
0 1.00 1.00 1.00 16
1 1.00 0.69 0.81 16
2 0.72 1.00 0.84 13
avg / total 0.92 0.89 0.89 45
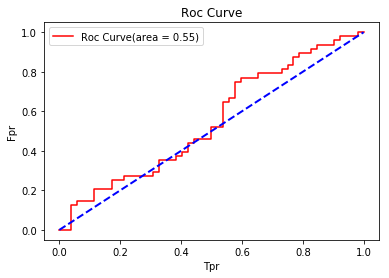
roc、AUC例子:(用random生成随机数,所以效果较差)
import numpy as np
import random
from sklearn import metrics
import matplotlib.pyplot as plt
%matplotlib inline
y_true = np.random.randint(1,3,size=100)
y_score = [np.random.random() for i in range(100)]
fpr, tpr, thresholds = metrics.roc_curve(y_true, y_score, pos_label=2)
auc_value = metrics.auc(fpr,tpr)
plt.plot(fpr, tpr, color="red", label="Roc Curve(area = %0.2f)" % auc_value)
print("Auc:",auc_value) #计算auc
plt.plot((0,1),(0,1), color="blue", linewidth=2, linestyle='--')
plt.legend(loc="best")
plt.title("Roc Curve")
plt.xlabel("Tpr")
plt.ylabel("Fpr")
Auc: 0.548076923077
<matplotlib.text.Text at 0xe2a97f390>

一般而言,Auc值处于0.5-1之间,曲线越靠近左上角越好,那么面积将越接近于1,效果越好。下图展现较好效果: