攻防世界-best_rsa

一、题目

给出两个公钥和两个密文

二、解题

1、

两个公钥，用Crypto库可以直接获取到n1,n2,e1,e2

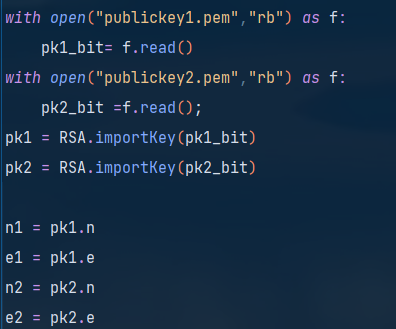
2、

但是仅有n和e和c无法解出明文，还需要有d，但是算d需要有p和q,打印n发现是个上百位的模数，通过暴力算法显然不当，因此弃用yafu。再到http://www.factordb.com/尝试分解，也没有结果

3、

正当一筹莫展的时候，打印n1和n2时发现n1和n2相同，两个不同的公钥，竟然巧合的存在相同的模数！？于是上网一查，发现对于这种情况可以使用共模攻击来绕过解密私钥，仅仅使用n,e1,e2,c1,c2即可破解两份密文！

共模攻击原理与算法：

欧几里得算法与欧几里得扩展算法

gmpy2库的运用

• gmpy2是一个用于Python的高精度计算库，支持大整数、有理数和浮点数的计算。你可以通过pip安装gmpy2，然后使用其提供的函数进行加减乘除运算，还可以进行三角函数、对数函数等高级计算
  
  参考:https://blog.csdn.net/m0_52842062/article/details/117852175

4、

万事具备，编写脚本解密即可
需要注意的是gmpy2的扩展欧几里得算法返回的是一个元组，其中s1和s2分别是元组的第二和第三个元素，而元组的第一个元素是gcd(s1,s2)，并不是我们需要的。

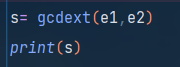
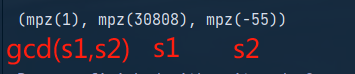
三、脚本代码与答案

from Crypto.PublicKey import RSA
from Crypto.Util.number import inverse,long_to_bytes,bytes_to_long
from gmpy2 import invert,gcd,gcdext

with open("publickey1.pem","rb") as f:
    pk1_bit= f.read()
with open("publickey2.pem","rb") as f:
    pk2_bit =f.read();
    
pk1 = RSA.importKey(pk1_bit)
pk2 = RSA.importKey(pk2_bit)

n1 = pk1.n
e1 = pk1.e
n2 = pk2.n
e2 = pk2.e
# print(n1)
# print(n2)


with open("cipher1.txt","rb") as f:
    c1= f.read()
with open("cipher2.txt","rb") as f:
    c2= f.read()

c1= bytes_to_long(c1)
c2= bytes_to_long(c2)

s= gcdext(e1,e2)
# print(s)

m = (pow(c1,s[1],n1)*pow(c2,s[2],n2) ) % n1
m = long_to_bytes(m)
print(m)

答案:flag{interesting_rsa}