攻防世界-不仅仅是RSA
一、题目
给出以下几个文件
py文件代码如下
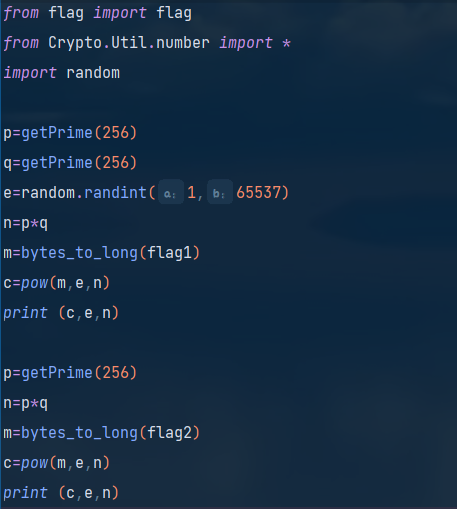
二、解题思路
1、听C1,C2的音频， 由长短声很快确定是摩斯密码，上网一搜，果然有在线摩斯密码音频解密网站,上去解密即可
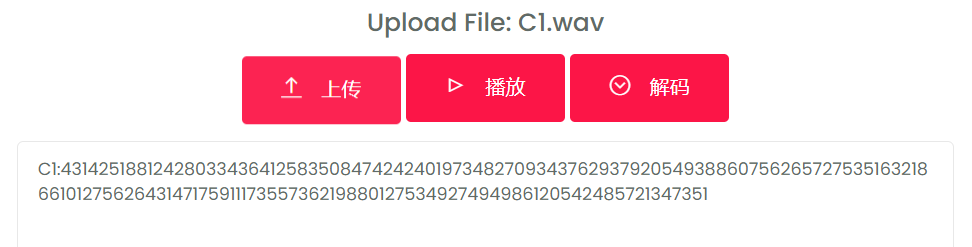
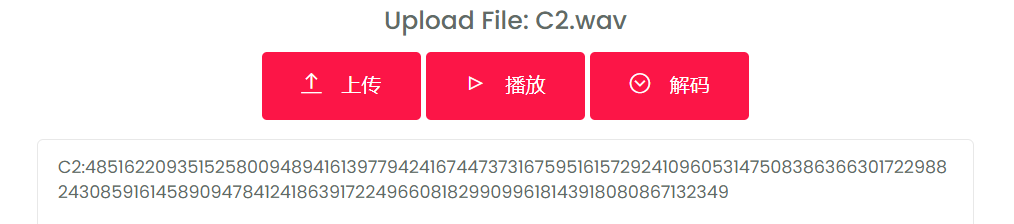
这里初步判断可能是密文
2、进一步分析代码
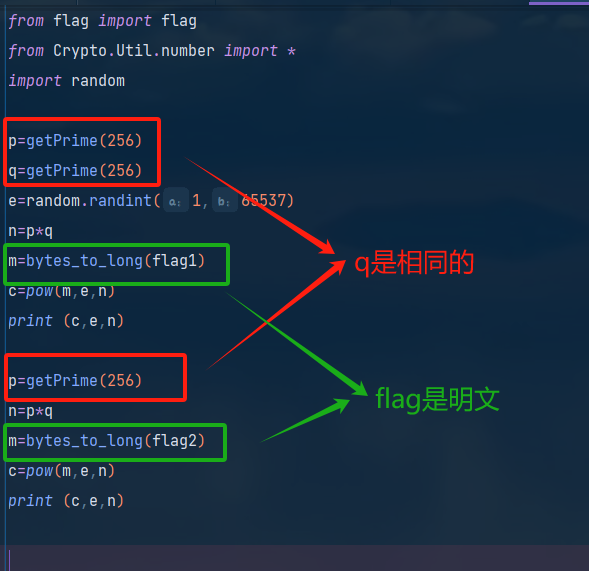
分析代码发现这就是一个简单的RSA加密算法，并且有两个不同公钥的RSA加密过程，
但是可以发现他们的n中都有一个共同的q，由于p和q都是素数，所以可以从求解n1和n2的最大公因式入手。
3、但是公钥都不知道，这时想起还有两个文件没有用到，这不就是公钥吗
上网一查发现“.pem”文件常常用来保存公钥，用文件查看器可以看到里面的公钥用base64的格式进行编码。
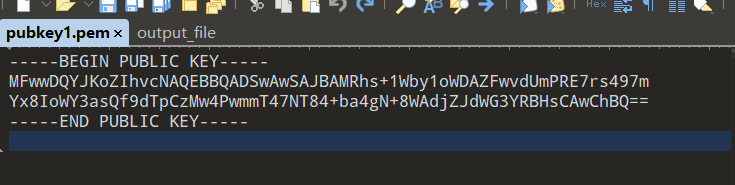
但是这里不进行解码，因为公钥只是一些无序的二进制数据，并没有什么实际的文本意义，python的Crypto.PublicKey库中的RSA模块提供公钥文件读取函数，直接调用即可读取入的公钥有n和e，用图示的办法可以分别调出它们。
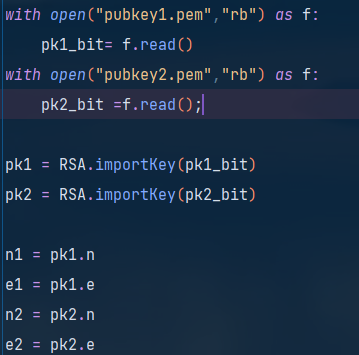
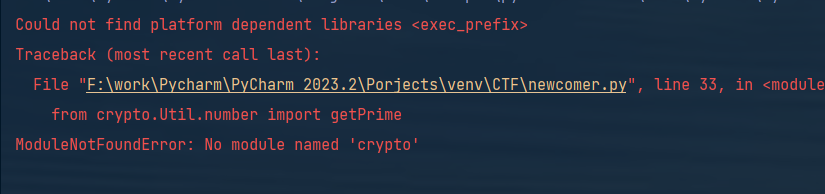
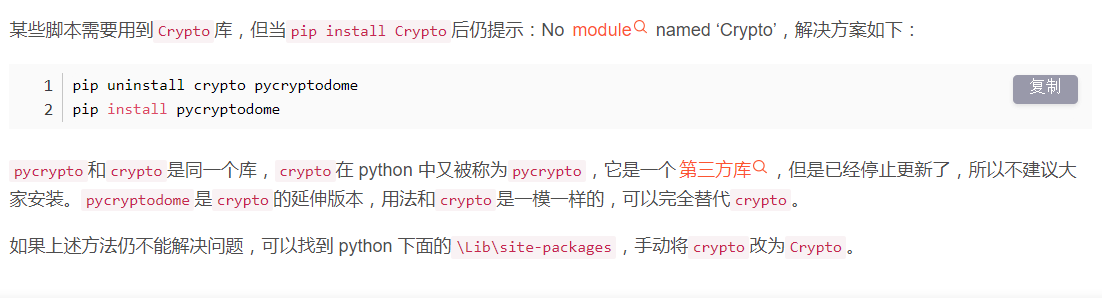
在安装Crypto库后出现了仍然无法调用库函数的情况
上网查了一下找到了解决办法:参考文章
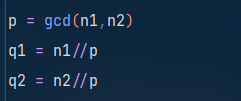
4、有了n1和n2，现在可以利用欧几里得辗转相除法求取n1和n2的最大公约数q，这样p1和p2就有了，一切都变得简单。
5、由于n=p*q，求解出q后就可以求解p1和p2，需要注意的是使用整除符号“//”而不是除号“/”。
解释:
- 普通除法 /：会返回一个浮动类型的结果，即使除数能够整除。
- 整数除法 //：返回一个整数结果，去掉小数部分。
这里可以验证一下，如果使用“/”，可以看到p的类型是浮点数，而“//”的结果中p的类型是整数：
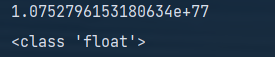
6、然后就是求解逆元d1和d2，最后利用d1和d2进行解密。第三方库中的inverse()函数就是求解逆元d的函数，参数为e和欧拉数phi,参数只能接收整数，这也是之前需要使用整除符号的原因。
phi = (p-1)*(q-1) 这时RSA的常识
7、利用私钥(n1,d1)和(n2,d2)解出明文m1和m2，再拼接即可得出flag
解密：m = e^d mod n
这里需要注意Crypto.Util.number库中的long_to_bytes模块，它是用来把这么一大串长数字转化为字节串显示。
补充:
- 字节串（bytes）是二进制数据的原始表示，每个字节表示一个数字值，范围从0到255。它们用于存储图像、音频、视频、加密密文等非文本类型的数据。这些字节可以是打印字符的编码，也可以是无法显示的控制字符或其他数据。
- 字节串中的每个字节都可以用 \x 后跟十六进制数字的形式表示，这些字节值不一定对应于可打印字符。
- print函数在打印字节串的时候会默认使用utf-8进行解码，如果字节串不能被utf-8正确解码，就会出现如下形式：
这时可能要如果出现这种情况，要么就是解密出现错误，要么就是密文并不是简单的文本形式，需要进行特殊的转化。
8、脚本代码
from Crypto.PublicKey import RSA
from Crypto.Util.number import inverse,long_to_bytes
with open("pubkey1.pem","rb") as f:
pk1_bit= f.read()
with open("pubkey2.pem","rb") as f:
pk2_bit =f.read();
pk1 = RSA.importKey(pk1_bit)
pk2 = RSA.importKey(pk2_bit)
n1 = pk1.n
e1 = pk1.e
n2 = pk2.n
e2 = pk2.e
c1 = 4314251881242803343641258350847424240197348270934376293792054938860756265727535163218661012756264314717591117355736219880127534927494986120542485721347351
c2 = 485162209351525800948941613977942416744737316759516157292410960531475083863663017229882430859161458909478412418639172249660818299099618143918080867132349
#求解两数的最大公约数
def gcd(a,b):
while(b!=0):
r=a%b
a=b
b=r
return a
p = gcd(n1,n2)
q1 = n1//p
q2 = n2//p
phi_1 = (p-1)*(q1-1)
phi_2 = (p-1)*(q2-1)
d1= inverse(e1,phi_1)
d2= inverse(e2,phi_2)
m1_bit = pow(c1,d1,n1)
m2_bit = pow(c2,d2,n2)
m1 = long_to_bytes(m1_bit)
m2 = long_to_bytes(m2_bit)
print(m1+m2)
9、最终答案
b'UNCTF{ac01dff95336aa470e3b55d3fe43e9f6}'
