7-1 哥尼斯堡的“七桥问题” （25 分）

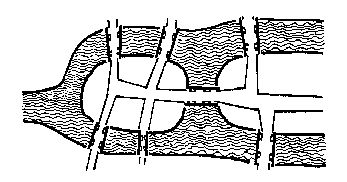
哥尼斯堡是位于普累格河上的一座城市，它包含两个岛屿及连接它们的七座桥，如下图所示。

可否走过这样的七座桥，而且每桥只走过一次？瑞士数学家欧拉(Leonhard Euler，1707—1783)最终解决了这个问题，并由此创立了拓扑学。

这个问题如今可以描述为判断欧拉回路是否存在的问题。欧拉回路是指不令笔离开纸面，可画过图中每条边仅一次，且可以回到起点的一条回路。现给定一个无向图，问是否存在欧拉回路？

输入格式:

输入第一行给出两个正整数，分别是节点数N (1)和边数M；随后的M行对应M条边，每行给出一对正整数，分别是该条边直接连通的两个节点的编号（节点从1到N编号）。

输出格式:

若欧拉回路存在则输出1，否则输出0。

输入样例1:

6 10
1 2
2 3
3 1
4 5
5 6
6 4
1 4
1 6
3 4
3 6

输出样例1:

1

输入样例2:

5 8
1 2
1 3
2 3
2 4
2 5
5 3
5 4
3 4

输出样例2:

0

#include<stdio.h>
#include<string.h>
int Nv,Ne;//只需要判断是否连通和度数就能做了 
int pre[1005];//连通集 
int degree[1005];//求每个顶点的度数 
int find(int x){ //查找老大 
    if(pre[x]!=x){
        pre[x] = find(pre[x]);
    }
    return pre[x];
}
void join(int x,int y){ //将两个点连通 
    int fx = find(x);
    int fy = find(y);
    if(fx!=fy){
        pre[fx] = fy;
    }
}
int main()
{
    int i;
    int a,b;//两个点 
    scanf("%d %d",&Nv,&Ne);
    for(i=0;i<Nv;i++){//初始化两个数组 
        pre[i] = i;
        degree[i] = 0;
    }
    for(i=0;i<Ne;i++){
        scanf("%d %d",&a,&b);
        a--;b--;
        join(a,b);
        degree[a]++; 
        degree[b]++;
    }
    int count=0;
    for(i=0;i<Nv;i++){
        if(pre[i]!=find(i)){
            count++;
        }
    }
    if(count==1){
        for(i=0;i<Nv;i++){
            if(degree[i]%2!=0){
                printf("0\n");
                return 0;
            }
        }
        printf("1\n");
    }else{
        printf("0\n");
    }

    return 0;
}